文章
<Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>注意</AlertTitle> <AlertDescription>本文暂未组织完善,仅作为草稿</AlertDescription> </Alert> 大家好啊,今天来点大家想看的东西啊。 世界上有很多门编程语言,每门语言都有着自己的优缺点,使用场景也各不相同。国内教学一般会选择 C 语言作为入门语言,后面再教 Java、Python 等。自己写了这么久的代码,接触过不少语言,总归是有一些想法的,在此分享一下。注意,本文属于杂谈,行文较为随意。 我是初中开始对编程感兴趣的,于是购买了《C 语言从入门到精通》这本书 —— 然后写完 Hello World 就再也没看过了。只能说还是太小吧,思考能力还是不够,以及教材本身的落后。落后在哪我真的很难说,国内的大多数教材总是严重滞后于生产实际,这大家有目共睹。就开发工具来说,书中推荐的是 Visual Studio 6.0,我嘞个老东西啊。 回到 C 语言本身,现在来谈一些缺点。是的,我其实并不喜欢 C 语言,虽说是高级语言,但它离底层实在是太近了,我觉得有点不够“高级”。 ## 字符串 C 语言中字符串的定义是这样的: ```c char s[6] = {'H', 'e', 'l', 'l', 'o', '\0'}; // 定义长度为 6 的字符串 char s2[5] = {'H', 'e', 'l', 'l', 'o'}; // 定义长度为 5 的字符串,未以 '\0' 结尾 ``` 在学 C 的时候,我就觉得字符串的处理实在是太麻烦了。C 语言中没有专门的字符串类型,字符串其实就是字符数组,结尾用一个特殊的空字符 `\0` 来标识结束。为什么?因为 C 语言是支持越界访问数组的,没有 `\0` 就不知道字符串在哪结束。 我们来对比一下 Python 中用 `list{:python}` 来模拟字符串的例子: ```python s = ['H', 'e', 'l', 'l', 'o'] # 定义长度为 5 的字符串 ``` 如果我们访问第六个元素 `s[5]{:python}`,Python 会抛出一个 `IndexError{:python}` 异常,告诉我们索引超出了范围。而在 C 语言中,访问 `s[5]{:c}` 我们能知道字符串该结束了,而访问 `s2[5]{:c}` 直接就是 [未定义行为](https://en.wikipedia.org/wiki/Undefined_behavior) 了,很可能出现安全漏洞和崩溃。 YouTube 视频 [The worst programming language of all time](https://www.youtube.com/watch?v=7fGB-hjc2Gc) 喷了两个小时的 C++,我要笑死了。 其实,正如 [Rust 程序设计语言](https://doc.rust-lang.org/stable/book/ch08-02-strings.html#strings-are-not-so-simple) 所说,字符串并不简单。你还需要去处理编码、Unicode 等问题,我想很少有人没有见到一堆乱码。 ## 修改传入的参数 先说结论:我坚决反对修改传进来的值。这种做法既不直观,也不安全,更违背了函数式编程的基本原则。 ```ts export const authOptions: NextAuthOptions = { callbacks: { jwt({ token, user }) { // The arguments user, account, profile and isNewUser are only passed the first time this callback is called on a new session, // after the user signs in. In subsequent calls, only token will be available. // token : The current JSON Web Token // user : The user object returned by the callback for the session (only available on first sign in) if (user) { token = { ...token, ...user }; } return token; }, session({ session, token }) { if (session.user == undefined) { session.user = {}; session.user.name = token.name; } else { session.user.name = token.name; } session.step = token.step; session.secretCode = token.secretCode; session.accessToken = token.accessToken; session.refreshToken = token.refreshToken; session.mfaSession = token.mfaSession; return session; }, }, }; ``` 在 C 语言中,参数传递有两种方式:按值传递和按指针传递。按值传递还好,至少不会影响到原始数据。但是按指针传递就麻烦了,你永远不知道一个函数会不会偷偷地修改你传进去的参数。 ```c void mysterious_function(int *arr, int size) { // 这个函数做了什么? // 它会修改数组内容吗? // 只有看实现才知道! } ``` 这种设计带来的问题是显而易见的: 1. 可读性差:仅从函数调用无法判断参数是否会被修改 2. 调试困难:当数据被意外修改时,很难追踪到是哪个函数干的 3. 副作用泛滥:函数不再是纯函数,而是充满了副作用的“黑盒” 更要命的是,C 语言没有 `const` 关键字的严格限制(早期版本),也没有明确的输入输出参数标记。你拿到一个函数,完全不知道它会对你的数据做什么。 ## undefined 还是 null? 在 JavaScript/TypeScript 中,我们有 `undefined{:ts}` 和 `null{:ts}`,他们到底有什么区别?我从接触到 JavaScript/TypeScript 开始就一直搞不清楚。 直到我认识到 `Map{:ts}` 这个数据结构,才在获取值时发现了两者的区别: ## 糟糕的 NullPointerException Java 语言中,`NullPointerException{:java}`(简称 NPE)是最常见的运行时错误之一。NPE 通常发生在你试图访问一个为 `null{:java}` 的对象的成员或方法时。 ```java String str = null; int length = str.length(); // 这里会抛出 NullPointerException ``` NPE 的问题在于它通常是在运行时才被发现的,这使得调试变得非常困难。更糟糕的是,NPE 可能会在程序的任何地方发生,导致程序崩溃或产生不可预期的行为。
经常有人问我该怎么学习编程语言,我的评价是:**从项目开始**。如果你不知道该做什么项目,就去学一门编程语言的话,只能是写一些无聊、枯燥的小的代码块,有的时候还会用一些莫名其妙的例子来举例。你说对学习有没有作用?当然有,但我并不认为这能为你以后做更大的项目有什么帮助。因为你以后写项目的时候自然会使用到需要学的语法,不如直接从项目开始。 话虽如此,这也是对已经有编程经验的人说的。如果你是一个完全没有编程经验的人,直接从项目开始可能会让你感到无从下手。对于这种情况,我建议先学习一些基础知识,很多编程语言都有自己的入门教程,或者可以参考一些在线课程。对语法有了大致了解之后,再去写项目。 对于更加进阶的设计模式(最常用的如单例模式)、变量不变性什么的,也都是各个项目总结出来的最佳实践。你可以在写项目的过程中逐渐体会到这些内容。不要急于求成,编程语言的学习是一个循序渐进的过程。 多使用搜索引擎和社区资源,如 Stack Overflow、GitHub 等,寻找解决方案和灵感。参与开源项目也是一个很好的学习方式,可以让你接触到真实的代码和项目结构。 对了,请务必保证“网络通畅”,你都学习编程语言了,怎么能没有科学工具呢? 最后,请务必学会使用版本控制系统(如 Git),它可以帮助你管理代码的变更,记录项目的进展,并且在遇到问题时可以轻松回退到之前的版本 —— [计算机教育中缺失的一课](/post/Missing-Semester),或者应该说是第零课,也有提到。
## Introducing "GeB": A Clear Decimal Counterpart to GiB We strongly recommend GeB over GB for all decimal-based contexts. 我们始终推荐在十进制语境中使用 GeB,而非 GB。 ## Background ## 背景 When measuring digital storage, we often encounter **GB** and **GiB**, but their meanings differ significantly: 在衡量数字存储空间时,我们常看到 **GB** 和 **GiB**,但它们实际意义大不相同: | Abbreviation 缩写 | Fullname 全称 | Bytes 字节数 | | | :---------------: | :-----------: | :----------------------: | :------------------------------: | | GiB | Gibibyte | $2^{30} = 1,073,741,824$ | Standardized by the IEC | | GiB | Gibibyte | $2^{30} = 1,073,741,824$ | IEC 二进制标准单位 | | GB | Gigabyte | $10^9 = 1,000,000,000$ | SI-defined, but ambiguously used | | GB | Gigabyte | $10^9 = 1,000,000,000$ | SI 十进制单位,但使用非常混乱 | This leads to confusion: storage vendors use GB, but operating systems show GiB. Users often feel shortchanged when numbers don't match. 这造成了大量误解:硬盘厂商标注 **GB**,但操作系统显示的是 **GiB**,用户总感觉“买亏了”。 ## Proposal: Introduce **GeB** ## 提案:引入 **GeB** We propose a new symbol: **GeB**, standing for **G**id**e**byte (**G**iga-d**e**cimal Byte), as a clean, unambiguous counterpart to **GiB**, standing for **G**ib**i**byte (**G**iga-b**i**nary Byte). 为了消除 GB 和 GiB 之间的混乱,我们提出一个新的缩写:**GeB**,表示 **G**id**e**byte(十进制千兆字节),与 **GiB** 这一表示 **G**ib**i**byte(二进制千兆字节)对称又清晰的一对单位。 | Abbreviation 缩写 | Fullname 全称 | Base 进制 | Bytes 字节数 | | :---------------: | :-----------: | :-------: | :--------------------------: | | GeB | Gidebyte | 10 | $(10^{3})^3 = 1,000,000,000$ | | GiB | Gibibyte | 2 | $(2^{10})^3 = 1,073,741,824$ | ## Pronunciation Across Languages ## 不同语言的发音 Abbreviations like GB, GiB, and GeB can be confusing not only in meaning but also in pronunciation. Different language communities handle technical acronyms differently, which may lead to confusion when discussing storage units. 类似 GB、GiB 和 GeB 这样的缩写,不仅意义容易混淆,发音在不同国家也存在差异。以下是一些主流语言环境的常见处理方式: | [BCP 47] | ~~GB~~ | <ins>GiB</ins> | _GeB_ | Method 处理方式 | | :-----------------: | :--------: | :------------: | :--------: | :-----------------------------: | | en (English) | /dʒiːbiː/ | /gɪb/ | /gæb/ | As Word[^1] 作为单词[^2] | | ge (Germân) | Giga-Byte | Gibi-Byte | Gide-Byte | Read Fullname 念出全称 | | ja(日本語) | ジービー | ギブ | ゲブ | Copy English 照搬英语 | | zh-Hans(简体中文) | G-B | G-I-B | G-B | A Pronounce Separately 拆开拼读 | | zh-Hant(繁体中文) | 吉比(特) | 吉比(特) | 格比(特) | Remix zh-Hans 简繁混用 | [BCP 47]: https://www.rfc-editor.org/info/bcp47 [^1]: GB in [Initialism](https://simple.wikipedia.org/wiki/Initialism), others in [Acronym](https://en.wikipedia.org/wiki/Acronym). [^2]: GB 是 [Initialism](https://simple.wikipedia.org/wiki/Initialism),其他则是 [Acronym](https://simple.wikipedia.org/wiki/Acronym). ### Our Recommendation ### 我们的建议 We recommend that developers, technical writers, and system designers: 我们建议开发者、技术文档作者及系统设计者: - Replace ambiguous "GB" with **GeB** wherever decimal values are intended - 遇到十进制值时,统一使用 **GeB**,避免 GB 歧义 - Educate users through UI tooltips or documentation: $1 \mathrm{GeB} = 10^9 \mathrm{Bytes}$ - 通过界面提示或文档解释 $1 \mathrm{GeB} = 10^9 \mathrm{Bytes}$ - Align with the GiB/Geb pair in APIs and interfaces for better clarity - 在 API 和用户界面中采用 GiB/GeB 成对呈现,提高一致性 ## Beyond GeB: A Whole Family of Decimal Units ## 延伸 GeB:十进制单位家族 The same pattern can apply to other SI-prefixed units. Here’s a proposed decimal units family: 相同的模式可以适用于其他 SI 单位。这是一个拟议十进制单位家族: | Decimal 十进制 | | | | Binary 二进制 | | | | :------------: | :-----------: | :----: | :---------------: | :-------------: | :-----------: | :-------------: | | Value 值 | Fullname 全称 | SI | **Proposal 提案** | Value 值 | Fullname 全称 | **IEC 60027-2** | | $(10^3)^1$ | Kilobyte | **k**B | K**e**B | $(2^{10})^1$ | Kibibyte | K**i**B | | $(10^3)^2$ | Megabyte | MB | M**e**B | $(2^{10})^2$ | Mebibyte | M**i**B | | $(10^3)^3$ | Gigabyte | GB | G**e**B | $(2^{10})^3$ | Gibibyte | G**i**B | | $(10^3)^4$ | Terabyte | TB | T**e**B | $(2^{10})^4$ | Tebibyte | T**i**B | | $(10^3)^5$ | Petabyte | PB | P**e**B | $(2^{10})^5$ | Pebibyte | P**i**B | | $(10^3)^6$ | Exabyte | EB | E**e**B | $(2^{10})^6$ | Exbibyte | E**i**B | | $(10^3)^7$ | Zettabyte | ZB | Z**e**B | $(2^{10})^7$ | Zebibyte | Z**i**B | | $(10^3)^8$ | Yottabyte | YB | Y**e**B | $(2^{10})^8$ | Yobibyte | Y**i**B | | $(10^3)^9$ | Ronnabyte | RB | R**e**B | $(2^{10})^9$ | Robibyte | R**i**B | | $(10^3)^{10}$ | Quettabyte | QB | Q**e**B | $(2^{10})^{10}$ | Quebibyte | Q**i**B | This symmetry improves consistency and provides a clear mental model for interpreting storage sizes. 这样一来,单位对称统一,规则明确,便于理解与记忆。 > Note: In line with SI conventions, we use **k**B for $10^3$ bytes. Though **K**B is commonly seen, it's technically incorrect. > > 注:根据 SI 规范,$10^3$ 字节应写作 **k**B,虽然实际中常见写法为 **K**B,但那是不规范的。 ## Implementation & Adoption ## 推广建议 To encourage adoption: 鼓励采用: - Use **GeB** in developer tools, file explorers, and documentation - 在开发工具、系统界面、文件管理器中使用 **GeB** - Clarify unit meanings explicitly in software UIs - 项目文档中教育用户和贡献者,说明 GiB 与 GeB 的区别 - Encourage open-source libraries to support config options like: `formatSize(value, { unit: 'GeB' }){:ts}` - 推动开源库支持配置项:`formatSize(value, { unit: 'GeB' }){:ts}` ## Conclusion ## 结语 It’s time to clean up our units — for clarity, consistency, and communication. 是时候给计算机单位一套干净、统一、可说清楚的命名方式了。 Let’s make **GeB** the official decimal twin of **GiB**, and stop guessing how many bytes you really got. 让我们将 GeB 定为 GiB 的官方十进制“孪生兄弟”,别再猜自己到底得到了多少字节了, **Clear units. Clean minds. GeB it.** **让单位清晰,从此刻开始。**
## 开始 在写本网站时我曾对 [Prettier](https://prettier.io) 和 [ESLint](https://eslint.org) 的混合使用感到困惑,在查了相关资料后,我在项目 README.md 中这样记述: ### Is Prettier Feature Conflicting with ESLint? ### Prettier 的功能和 ESLint 冲突了吗? While configuring tools to improve code quality, I was unsure whether I should use Prettier or ESLint for handling the sorting of imports, properties, and Tailwind CSS classes. 在使用配置工具提高代码质量的过程中,我不太确定该使用 Prettier 还是 ESLint 来处理导入、属性和 Tailwind CSS 类名的排序。 Although Prettier plugins like [prettier-plugin-tailwindcss](https://github.com/tailwindlabs/prettier-plugin-tailwindcss) and [prettier-plugin-sort-imports](https://github.com/trivago/prettier-plugin-sort-imports) can address this, I don't consider them the "best practice". 虽然一些 Prettier 插件如 [prettier-plugin-tailwindcss](https://github.com/tailwindlabs/prettier-plugin-tailwindcss) 和 [prettier-plugin-sort-imports](https://github.com/trivago/prettier-plugin-sort-imports) 能处理,但我不认为他们是“最佳实践”。 As discussed in this [GitHub Issue](https://github.com/prettier/prettier/issues/2460) and this [Reddit Post](https://www.reddit.com/r/typescript/comments/15lr8p1/sorting_imports_eslint_vs_prettier), sorting can introduce side effects. Therefore, it's better to handle sorting with ESLint. 据这个 [GitHub Issue](https://github.com/prettier/prettier/issues/2460) 和这个 [Reddit 帖子](https://www.reddit.com/r/typescript/comments/15lr8p1/sorting_imports_eslint_vs_prettier) 讨论的内容,排序会引入副作用,因此更适合使用 ESLint 来处理排序。 Moreover, Prettier will not warn you about incorrect order, but ESLint will, as this is exactly what ES**Lint** is supposed to do. 不仅如此,Prettier 不会警告你错误的排列顺序,但 ESLint 会,因为这正是一个 ES**Lint** 该做的。 ## 再思考 根据 [此博客](https://antfu.me/posts/why-not-prettier-zh) 的记述,Prettier 和 ESLint 确实“并没有让你的生活变得更简单”,相反,为了处理它们之间的冲突,你需要花费更多的时间来配置它们。 所以以后我会考虑使用 ESLint 来处理所有的代码格式化问题。
计算机网络很有意思,然而曾经的教学方式让我对它产生了厌恶感,这是令人悲哀的,我喜欢从现实出发,而不是从书本出发。 让我们先列个表,看看自己所拥有的设备都支持哪些网络连接方式。 ## 设备清单 | 设备 | 型号 | 有线 | Wi-Fi 世代 | 简要备注 | | :------------: | :----------------------: | :------------------: | :-------------------: | :--------------------------------------------------------: | | 手机 | [Redmi K70] | - | Wi-Fi 7[^1]、Wi-Fi 6E | MLO;MIMO 2x2;[同步双频] | | 平板 | [iPad Pro 2021 11 inch] | - | Wi-Fi 6E | 2.4G、5G [同步双频];MIMO 80 MHz | | Mac | [Mac mini M4] | RJ45 千兆网口 | Wi-Fi 6E | - | | ~~笔记本电脑~~ | ~~[拯救者 R7000P 2021]~~ | ~~RJ45 千兆网口~~ | ~~Wi-Fi 6~~ | - | | 台式电脑 | DIY | 单 RJ45 2.5 G 网口 | Wi-Fi 7 | - | | 光猫 | H3-2sLite | 四 RJ45 千兆 LAN 口 | 不需要在意 | - | | ~~主路由器~~ | ~~[锐捷 RG-MA3063]~~ | ~~四 RJ45 千兆网口~~ | ~~Wi-Fi 6~~ | ~~最高 3000 Mb/s;MIMO 2x2;四网口任一作 WAN 口~~ | | 主路由器 | [小米 AX3000T] | 四 RJ45 千兆网口 | Wi-Fi 6 | 最高 574 + 2402 ≈ 3000 Mb/s;MIMO 2x2;四网口任一作 WAN 口 | | 副路由器 | [斐讯 K2] | 五 RJ45 百兆网口 | Wi-Fi 5 | 最高 1200 Mb/s;五网口其一固定 WAN 口 | [^1]: Wi-Fi 7 相关功能需 OTA 升级后开放,具体时间需待有关监管部门批准后推送 [Redmi K70]: https://www.mi.com/redmi-k70/specs [iPad Pro 2021 11 inch]: https://support.apple.com/zh-cn/111897 [Mac mini M4]: https://support.apple.com/zh-cn/121555 [拯救者 R7000P 2021]: https://item.lenovo.com.cn/product/1013207.html [锐捷 RG-MA3063]: https://www.acwifi.net/21472.html [小米 AX3000T]: https://www.mi.com/xiaomi-ax3000t [斐讯 K2]: https://product.yesky.com/product/977/977854/param.shtml [同步双频]: #双频合一与同步双频 ## 参考信息 提前声明:本文内容仅供参考,请以信息来源为准。 ### 有关比特、字节、速率的换算 - 换算关系 - 1 Byte = 8 bit - 通信等领域 - 1 KB = 1000 Byte - 1 MB = 1000 KB - 1 GB = 1000 MB - 计算机储存 - 1 KiB = 1024 Byte - 1 MiB = 1024 KiB - 1 GiB = 1024 MiB - 常见速率 - 100 Mb/s = 12.5 MB/s = 11.921 MiB/s - 1000 Mb/s = 125 MB/s = 119.21 MiB/s - 10000 Mb/s = 1.25 GB/s = 1.164 GiB/s 个人很讨厌使用 bit 而不是 Byte 来表示速率,一点都不直观,也讨厌千进制。 ### Wi-Fi 世代 下表来自 [维基百科](https://zh.wikipedia.org/wiki/Wi-Fi#%E4%B8%96%E4%BB%A3): | Wi-Fi 世代 | IEEE 标准 | 年份 | 最大速率 | 频段 GHz | | :--------: | :--------: | :------: | :-----------: | :-------: | | Wi-Fi 4 | [802.11n] | 2009 | 75 MB/s | 2.4、5 | | Wi-Fi 5 | [802.11ac] | 2013 | 867 MB/s | 5[^2] | | Wi-Fi 6 | [802.11ax] | 2021 | 1.2 GB/s | 2.4、5 | | Wi-Fi 6E | [802.11ax] | 2021 | 1.2 GB/s | 6[^3] | | Wi-Fi 7 | [802.11be] | 2024[^4] | 2.88 GB/s[^5] | 2.4、5、6 | | Wi-Fi 8 | [802.11bn] | ~~2028~~ | 12.5 GB/s | 2.4、5、6 | [^2]: Wi-Fi 5 仅指定在 5 GHz 频段的操作,2.4 GHz 频段的操作由 Wi-Fi 4 指定 [^3]: Wi-Fi 6E 是指在 6 GHz 频段运行的 Wi-Fi 设备的行业名称,其提供了 Wi-Fi 6 的功能和特性并扩展到 6 GHz 频段 [^4]: Wi-Fi 联盟在 2024 年开始认证 Wi-Fi 7 设备,但截至 2025 年 1 月,Wi-Fi 7 尚未被正式批准 [^5]: 中文维基百科给出的数值已经过时,以英文维基百科为准 [802.11n]: https://zh.wikipedia.org/wiki/IEEE_802.11n [802.11ac]: https://zh.wikipedia.org/wiki/IEEE_802.11ac [802.11ax]: https://zh.wikipedia.org/wiki/Wi-Fi_6 [802.11be]: https://zh.wikipedia.org/wiki/Wi-Fi_7 [802.11bn]: https://zh.wikipedia.org/wiki/IEEE_802.11bn - 在此注意 Wi-Fi 6 即我们目前最常用的 Wi-Fi 世代即可,而 Wi-Fi 7 的就属于战未来的了 - 且在中国大陆,6 GHz 的频段尚未开放 —— 也有可能永远不会开放 🤗 ### Wi-Fi 速率 参见 [此视频](https://www.bilibili.com/video/av787776505): Wi-Fi 最大速率 $=$ 编码方式 $\times$ 码率 $\times$ 最大信道有效子载波数量 $\times$ 单位时间符号传输数量 $\times$ 空间流数量 以 Wi-Fi 6 与 Wi-Fi 7 为例,其最大速率计算如下: | Wi-Fi 世代 | 调制方式 | 编码方式 | 码率 | 带宽 | 单位时间符号传输数量 | 空间流数量 | 最大速率 | | :--------: | :------: | :------: | :--: | :-----: | :------------------: | :--------: | :-------: | | Wi-Fi 6 | 1024-QAM | 10 | 5/6 | 160 MHz | 73529 | MIMO 8x8 | 1.2 GB/s | | Wi-Fi 7 | 4096-QAM | 12 | 5/6 | 320 MHz | 73529 | MIMO 8x8 | 2.88 GB/s | - 大多数设备为 MIMO 2x2,也即对应 300 MB/s 和 720 MB/s - 有关调制方式参见 [此视频](https://www.bilibili.com/video/av113683137041105) 其实 [Wi-Fi 6 英文维基百科](https://en.wikipedia.org/wiki/Wi-Fi_6#Rate_set) 给出了单空间流最大速率表格,其相比于中文维基百科的更为简洁。 ### 双频合一与同步双频 双频合一,又称双频优选,需要支持~~即时~~同步双频 RSDB 或并发双频 SDB 的设备,指路由器同时开启 2.4 GHz 和 5 GHz 两个频段,让设备自行选择连接的频段。 总之是狗屎,不要用,而且它们的措辞还总是混合在一起,具体看看这个 [知乎回答](https://www.zhihu.com/question/355416265/answer/891769324),不懂也没关系。 ### 以太网 Ethernet | 速度 | 非正式名称 | IEEE 标准 | 线缆类型 | 最大传输距离 m | | :------: | :-----------: | :-------: | :------: | :------------: | | 10 Mb/s | [10BASE-T] | 802.3 | 双绞线 | 100 | | 100 Mb/s | 100BASE-T | 802.3u | 双绞线 | 100 | | 1 Gb/s | [1000BASE-LX] | 802.3z | 光纤 | 5000 | | 1 Gb/s | [1000BASE-T] | 802.3ab | 双绞线 | 100 | | 2.5 Gb/s | [2.5GBASE-T] | 802.3bz | 双绞线 | 100 | | 5 Gb/s | [5GBASE-T] | 802.3bz | 双绞线 | 100 | | 10 Gb/s | [10GBASE-T] | 802.3an | 双绞线 | 100 | [10BASE-T]: https://zh.wikipedia.org/wiki/10BASE-T [1000BASE-LX]: https://zh.wikipedia.org/wiki/吉比特以太网#1000BASE-LX [1000BASE-T]: https://zh.wikipedia.org/wiki/吉比特以太网#1000BASE-T [2.5GBASE-T]: https://zh.wikipedia.org/zh-cn/2.5GBASE-T與5GBASE-T [5GBASE-T]: https://zh.wikipedia.org/zh-cn/2.5GBASE-T與5GBASE-T [10GBASE-T]: https://zh.wikipedia.org/wiki/10吉比特乙太網路#10GBASE-T ### 双绞线 CAT 下表来自 [此视频](https://www.bilibili.com/video/av459211809): | 规格 | 常规屏蔽模式 | 常规线规 AWG | 带宽 MHz | 100 Mb/s | 1 Gb/s | 2.5 Gb/s | 5 Gb/s | 10 Gb/s | | :------: | :----------: | :----------: | :------: | :------: | :----: | :------: | :----: | :-----: | | [CAT-5] | UTP | 24 | 100 | 🉑 | | | | | | [CAT-5e] | UTP | 24 | 125 | 🉑 | 🉑 | 不稳定 | 不稳定 | | | [CAT-6] | UTP 或 STP | 23 | 250 | 🉑 | 🉑 | 🉑 | 不稳定 | 55 m | | [CAT-6A] | STP | 23 | 500 | 🉑 | 🉑 | 🉑 | 🉑 | 🉑 | | [CAT-7] | S/FTP | 23 | 600 | 🉑 | 🉑 | 🉑 | 🉑 | 🉑 | | [CAT-7A] | S/FTP | 22 | 1000 | 🉑 | 🉑 | 🉑 | 🉑 | 🉑 | [CAT-5]: https://zh.wikipedia.org/wiki/CAT-5 [CAT-5e]: https://zh.wikipedia.org/wiki/CAT-5#Category_5e [CAT-6]: https://zh.wikipedia.org/wiki/CAT-6 [CAT-6A]: https://zh.wikipedia.org/wiki/CAT-6#Category_6A [CAT-7]: https://zh.wikipedia.org/wiki/CAT-7 [CAT-7A]: https://zh.wikipedia.org/wiki/CAT-7#Class_FA - 超过 CAT-6A 线请考虑光纤 自己找到一根双绞线,上面写着 `AMPHENGKE CAT5E UTP 24AWG 4PAIR AWM 2835 60°C FT4 VERIFIED MADE IN CHINA 063 M`,其中 AMPHENGKE 为~~某不知名~~品牌,规格为 CAT-5e,线规为 24 AWG,最高温度为 60 °C,FT4 为 CSA 防火等级,VERIFIED 表示已验证,MADE IN CHINA 为产地,063 M 为长度标定以方便切割。 ## 网络互联 这里先提前说明一点,网络配置属实困难,光是我们上面的参考信息就占了很多篇幅,一些相关的计算机网络知识也并未在此列出,以及想法很多时候都只是想法,真要实际操作起来,还是会遇到很多问题的。就目前我家的网络配置来说,这并未是一个经过深思熟虑的结果,一些难以解决的问题 —— 比如墙内预埋线的规格问题 —— 也只能暂时搁置,等以后有能力、有财力再来解决。 我现在家里办理的是 1000 Mb/s 的光纤宽带,屋外的光纤线熔接与尾纤后接入光猫,光猫再通过 CAT-5e 网线连接主路由器的 LAN1 口自动作为 WAN 口,主路由器的 LAN2 口连接副路由器的 WAN 口,主路由器的 LAN3 口连接 [Mac mini M4](#设备清单) 的 RJ45 网口。 ## 本地域名 首先要注意的一点是,在使用域名连接到本地时,请使用 `localhost`,几乎所有设备都会将其自动与 IPv4 下的 `127.0.0.1` 或 IPv6 下的 `::1` 绑定。 在 [多设备协同与自定义](/post/Multi-Device-Collaboration-And-Customize#桌面自定义) 中也有提到,IP 的变化是会令人难受的,固定 IP 虽然能解决该问题,但一是这要求你对路由器有管理权,二是路由器要具备能固定 IP 的功能,再就是一旦换到另一个局域网,就又得重新设置。而本地域名则不会有这些问题。 本地域名怎么获取呢?macOS 和 Windows 均使用 `hostname{:bash}` 命令即可,结果分别是 `Mac-mini.local` 和 `Cierra_Runis`。 当然,这里给一下 [保留 IP 地址](https://zh.wikipedia.org/zh-cn/%E4%BF%9D%E7%95%99IP%E5%9C%B0%E5%9D%80) 和 [IPv6 地址分配情况](http://comeround.cn/article/ipv6-address.html) 的链接,请自行查阅。为 [安全起见](http://hello.fe80.cn/pages/ipv6/i6.html) 请不要把保留 IP 地址外的地址公布 —— 由于 IPv6 的分配被严格管理,可以查到你设备的位置,我自己查能精确到县级。 下表来自 `ifconfig{:bash}` 和 `ipconfig /all{:bash}` 命令: | 设备 | IP | 类型 | | :----------------: | :-------------------------------: | :----------------: | | Mac mini | ☀️192.168.2.69/24 | IPv4 局域网私有 IP | | Mac mini | 🌞fe80::8bc:15d5:9bc3:9771%en1/64 | IPv6 链路本地地址 | | 拯救者 R7000P 2021 | 🌕192.168.2.75/24 | IPv4 局域网私有 IP | | 拯救者 R7000P 2021 | 🌝fe80::98b4:7a27:b5c0:d12f%18/64 | IPv6 链路本地地址 | - 这里不知道为什么是 %en1 而下面是 %9,根据 [维基百科](https://zh.wikipedia.org/wiki/IPv6#cite_ref-rfc4007_7-0) 和 [RFC 4007](https://datatracker.ietf.org/doc/html/rfc4007#section-11.2),不同的操作系统有着不同的命名。 就我自己,在 Mac mini 和拯救者 R7000P 2021 搭配 Clash Verge 虚拟网卡开启及关闭时,使用 `ping{:bash}` 命令得到以下结果: | 操作系统 | 测试域名 | ping 显示域名 | 双方皆关闭 | 双方皆打开 | 结果 | | :---------: | :--------------------: | :----------------: | :---------: | :-------------: | :--: | | macOS | _Mac_ | mac.lan | 198.18.1.87 | 198.18.1.87 | 💢 | | macOS | _Mac.lan_ | mac.lan | 198.18.1.87 | 198.18.1.87 | 💢 | | macOS | _Mac.local_ | - | - | - | 💩 | | Windows | _Mac_ | Mac.lan | ☀️ | ☀️ | 💔 | | Windows | _Mac.lan_ | Mac.lan | ☀️ | 198.18.0.69[^6] | 💢💢 | | Windows | _Mac.local_ | Mac.local | - | 198.18.0.70[^6] | 💢💢 | | macOS | ~~Mac-mini~~ | mac-mini.lan | 198.18.1.83 | 198.18.1.83 | 💢 | | macOS | ~~Mac-mini.lan~~ | mac-mini.lan | 198.18.1.83 | 198.18.1.83 | 💢 | | macOS | ~~Mac-mini.local~~ | mac-mini.local | 127.0.0.1 | 127.0.0.1 | 😄 | | Windows | **Mac-mini** | Mac-mini.local | 🌞%9 | 🌞%9 | 🚀 | | Windows | **Mac-mini.lan** | Mac-mini.lan | - | 198.18.0.71[^6] | 💢💢 | | **Windows** | **Mac-mini.local** | Mac-mini.local | 🌞%9 | 198.18.0.72[^6] | 💢💢 | | **macOS** | **Cierra_Runis** | cierra_runis.lan | 198.18.1.82 | 198.18.1.82 | 💢 | | macOS | **Cierra_Runis.lan** | cierra_runis.lan | 198.18.1.82 | 198.18.1.82 | 💢 | | macOS | **Cierra_Runis.local** | cierra_runis.local | 🌕 | 🌕 | 🚀 | | Windows | ~~Cierra_Runis~~ | Cierra_Runis | 🌝%18 | 🌝%18 | 😄 | | Windows | ~~Cierra_Runis.lan~~ | Cierra_Runis.lan | 🌕 | 198.18.0.73[^6] | 💢💢 | | Windows | ~~Cierra_Runis.local~~ | Cierra_Runis | 🌝%18 | 🌝%18 | 😄 | [^6]: Clash Verge 导致连续的 IP 地址变化 - 删除线部分为不需要的测试,请使用 `localhost` 代替 - 加粗部分为重要测试 - 斜线部分为不确定是否能在其他局域网复现的测试 - 💢: 不可用的 198.18.x.x 网段 - 💩: 完全不通 - 💔:此域名为路由器后台设备列表名称 - 💢💢:不可用的 198.18.x.x 网段且两次结果不一样 - 😄:“你老惦记你那本地域名干什么?那我缺的这个 `localhost` 谁给我补啊?” 总结下来,两个最重要的测试,四个结果只有一个可用,有点尴尬了。 而最后的结果很明显,Mac mini 给出的域名要去掉 `.local` 给 Windows 使用,而 Windows 反过来 —— 什么极限换家? ### Windows 与 macOS 在本地域名上的差异 在 Windows 上,使用 `hostname{:bash}` 命令得到的结果是设备名称,这可以通过 `设置 > 系统` 查看并修改 —— 在此我修改为 `Laptop`。 更新 Mac 版本后 `hostname{:bash}` 给出 `Mac.lan`。据查,有下表: | 命令 | 输出 | 备注 | | :---------------------------------: | :-----------------: | :-------------------------------------------------------: | | `hostname{:bash}` | Mac.lan | 使用 `fastfetch{:bash}` 会看到 `Mac` | | `scutil --get HostName{:bash}` | HostName: not set | - | | `scutil --get LocalHostName{:bash}` | Mac-mini | 在 `系统设置 > 共享` 能看到,接续的 `.local` 是无法更改的 | | `scutil --get ComputerName{:bash}` | 某不科学の Mac mini | 在 `系统设置 > 关于本机` 能看到 | 我们测试最终结果是: | 操作系统 | 测试域名 | ping 显示域名 | 双方皆打开 | | :------: | :------------: | :------------: | :--------------: | | macOS | Laptop | laptop.lan | 🌕 | | macOS | Laptop.lan | laptop.lan | 🌕 | | macOS | Laptop.local | laptop.local | 🌕 | | Windows | Mac-mini | Mac-mini.local | 🌞%9 | | Windows | Mac-mini.lan | Mac-mini.lan | 198.18.0.127[^6] | | Windows | Mac-mini.local | Mac-mini.local | 198.18.0.129[^6] | 因而我们在 [本地域名](#本地域名) 一节中给出的结论仍然适用。 补充一下,在路由器后台能看到设备列表中,Windows 设备的名称变为了 `Laptop`,而 Mac mini 的名称是 `Mac`。 尝试使用 `sudo scutil --set HostName 'Mac-mini.local'{:bash}` 并重启机器看看结果又会如何 —— 答案是测试结果毫无变化,而前一张表前两个输出都变为了 `Mac-mini.local` —— 记得使用 `sudo scutil --set HostName ''{:bash}` 重新清空。 ## DDNS 所以为什么要局限于本地域名呢?大家好啊,我是 DDNS,今天来点大家想看的东西啊。 IPv6 的解决了 IPv4 的问题,这种屁话略,首先保证光猫、路由器、设备都支持并开启 IPv6,保证能获取到 IPv6 地址。 本网站 `note-of-me.top` 的域名解析服务商是 [阿里云](https://www.aliyun.com),阿里云会附赠一个免费的域名解析服务,我们可以使用它来实现 DDNS。 首先我们得先获取到阿里云的 AccessKey ID 和 AccessKey Secret,具体操作略,总之要配置完 [阿里云 CLI](https://www.alibabacloud.com/help/zh/cli/installation-guide/) 工具。 <Accordion type='single' collapsible> <AccordionItem value='macos-ddns'> <AccordionTrigger>macOS `~/.local/bin/ddns`</AccordionTrigger> <AccordionContent> ```bash #!/bin/bash set -euo pipefail if ! command -v jq >/dev/null; then echo "Error: 'jq' is not installed. You can install it with 'brew install jq' on macOS." exit 1 fi if ! command -v aliyun >/dev/null; then echo "Error: 'aliyun' CLI is not installed. See https://github.com/aliyun/aliyun-cli for installation instructions." exit 1 fi # https://api.aliyun.com/document/Alidns/2015-01-09/AddDomainRecord DOMAIN_NAME="note-of-me.top" RR=$(scutil --get LocalHostName) # Use LocalHostName as prefix RECORD_TYPE="AAAA" IPV6_ADDR=$(ifconfig "$(route -n get -inet6 default | awk '/interface:/ {print $2}')" | awk '/inet6/ && !/fe80/ {print $2}' | grep -vE 'temporary|dynamic' | head -n1) if [ -z "$IPV6_ADDR" ]; then echo "[$(date '+%F %T')] No IPv6 address available" exit 1 fi RECORD_INFO=$(aliyun alidns DescribeSubDomainRecords \ --SubDomain "$RR.$DOMAIN_NAME" \ --Type "$RECORD_TYPE") RECORD_ID=$(echo "$RECORD_INFO" | jq -r '.DomainRecords.Record[0].RecordId // empty') RECORD_IP=$(echo "$RECORD_INFO" | jq -r '.DomainRecords.Record[0].Value // empty') echo "[$(date '+%F %T')] Current DNS: $RECORD_IP" if [ -n "$RECORD_ID" ]; then if [ "$RECORD_IP" = "$IPV6_ADDR" ]; then echo "[$(date '+%F %T')] IPv6 ($IPV6_ADDR) no changed" exit 0 fi echo "[$(date '+%F %T')] Updating $RR.$DOMAIN_NAME: $RECORD_IP => $IPV6_ADDR" aliyun alidns UpdateDomainRecord \ --RecordId "$RECORD_ID" \ --RR "$RR" \ --Type "$RECORD_TYPE" \ --Value "$IPV6_ADDR" >/dev/null else echo "[$(date '+%F %T')] Creating $RR.$DOMAIN_NAME => $IPV6_ADDR" aliyun alidns AddDomainRecord \ --DomainName "$DOMAIN_NAME" \ --RR "$RR" \ --Type "$RECORD_TYPE" \ --Value "$IPV6_ADDR" >/dev/null fi ``` </AccordionContent> </AccordionItem> <AccordionItem value='windows-ddns'> <AccordionTrigger>Windows `~\.local\bin\ddns.ps1`</AccordionTrigger> <AccordionContent> ```powershell # Requires: aliyun CLI 已配置好账号 # 修改以下参数 $DomainName = "note-of-me.top" $RR = $env:COMPUTERNAME # 或 [System.Net.Dns]::GetHostName() $RecordType = "AAAA" # 获取 IPv6 地址 function Get-PreferredIPv6Address { # 获取所有候选 IPv6 地址 $candidates = Get-NetIPAddress -AddressFamily IPv6 | Where-Object { $_.AddressState -eq "Preferred" -and $_.IPAddress -notmatch "^fe80" -and ([System.Net.IPAddress]::Parse($_.IPAddress).GetAddressBytes()[0] -band 0b11100000) -eq 0b00100000 } # 优先选择 DHCP 分配的地址 $target = $candidates | Where-Object { $_.PrefixOrigin -eq "Dhcp" -and $_.SuffixOrigin -eq "Dhcp" } | Select-Object -First 1 if (-not $target) { # 其次选择 RouterAdvertisement 分配但不是随机后缀的地址 $target = $candidates | Where-Object { $_.PrefixOrigin -eq "RouterAdvertisement" -and $_.SuffixOrigin -ne "Random" } | Select-Object -First 1 } if (-not $target) { Write-Host "[$(Get-Date -Format 'yyyy-MM-dd HH:mm:ss')] ❌ 未找到合适的 IPv6 地址" return $null } Write-Host "[$(Get-Date -Format 'yyyy-MM-dd HH:mm:ss')] ✅ 使用 IPv6 地址: $($target.IPAddress)" return $target.IPAddress } # 获取当前记录 $ipv6Addr = Get-PreferredIPv6Address $recordInfoRaw = & aliyun alidns DescribeSubDomainRecords ` --SubDomain "$RR.$DomainName" ` --Type "$RecordType" if (-not $recordInfoRaw) { Write-Host "[$(Get-Date -f 'yyyy-MM-dd HH:mm:ss')] Failed to get record info" exit 1 } $recordInfo = $recordInfoRaw | ConvertFrom-Json $record = $recordInfo.DomainRecords.Record | Select-Object -First 1 $recordId = $record.RecordId $currentIP = $record.Value Write-Host "[$(Get-Date -f 'yyyy-MM-dd HH:mm:ss')] Current DNS: $currentIP" if ($recordId) { if ($currentIP -eq $ipv6Addr) { Write-Host "[$(Get-Date -f 'yyyy-MM-dd HH:mm:ss')] IPv6 ($ipv6Addr) no changed" exit 0 } Write-Host "[$(Get-Date -f 'yyyy-MM-dd HH:mm:ss')] Updating $RR.$DomainName\: $currentIP => $ipv6Addr" & aliyun alidns UpdateDomainRecord ` --RecordId $recordId ` --RR $RR ` --Type $RecordType ` --Value $ipv6Addr | Out-Null } else { Write-Host "[$(Get-Date -f 'yyyy-MM-dd HH:mm:ss')] Creating $RR.$DomainName => $ipv6Addr" & aliyun alidns AddDomainRecord ` --DomainName $DomainName ` --RR $RR ` --Type $RecordType ` --Value $ipv6Addr | Out-Null } ``` </AccordionContent> </AccordionItem> </Accordion> ## 回到过去 两台设备直接使用网线连接,这就是最简单的局域网 —— 教程可参考 [此视频](https://www.bilibili.com/video/av424790900): 为了防止 Wi-Fi 影响我们这次实验,先关闭笔记本电脑和 Mac mini 的 Wi-Fi,然后使用一根 CAT-5e 的网线将它们连接起来,接着我们做一下简单的配置: | 笔记本电脑 | Mac mini | | :-------------------------: | :-------------------------: | | Windows 设置 | 系统设置 | | 网络和 Internet | 网络 | | 以太网 | 以太网 | | 编辑 | 详细信息 | | 选择手动 | 配置 IPv4 | | 打开 IPv4 | 选择手动 | | IP 地址填入 192.168.1.**1** | IP 地址填入 192.168.1.**2** | | 子网掩码填入 255.255.255.0 | 子网掩码填入 255.255.255.0 | 这样我们就有了以下的局域网拓扑图: ```mermaid graph LR L(拯救者 R7000P 2021<br/>IPv4 192.168.1.1) M4(Mac mini M4<br/>IPv4 192.168.1.2) L <-- "CAT-5e" --> M4 ``` 由于两个设备的 RJ45 接口和 CAT-5e 网线都支持 1000 Mb/s,我们可以使用 [iperf3](https://github.com/esnet/iperf) 来测试两台设备之间的最大传输速率: 在 Mac mini 使用 `iperf3 -s{:bash}` 开启服务器,在笔记本电脑上使用 `iperf3 -c 192.168.1.2{:bash}` 连接服务器,测试结果如下: <Accordion type='single' collapsible> <AccordionItem value='iperf3-test'> <AccordionTrigger>正向测试</AccordionTrigger> <AccordionContent> ```powershell PS > iperf3 -c 192.168.1.2 Connecting to host 192.168.1.2, port 5201 [ 5] local 192.168.1.1 port 55591 connected to 192.168.1.2 port 5201 [ ID] Interval Transfer Bitrate [ 5] 0.00-1.01 sec 117 MBytes 976 Mbits/sec [ 5] 1.01-2.01 sec 113 MBytes 944 Mbits/sec [ 5] 2.01-3.01 sec 113 MBytes 945 Mbits/sec [ 5] 3.01-4.01 sec 112 MBytes 940 Mbits/sec [ 5] 4.01-5.01 sec 113 MBytes 949 Mbits/sec [ 5] 5.01-6.01 sec 113 MBytes 946 Mbits/sec [ 5] 6.01-7.01 sec 112 MBytes 948 Mbits/sec [ 5] 7.01-8.01 sec 113 MBytes 950 Mbits/sec [ 5] 8.01-9.01 sec 113 MBytes 944 Mbits/sec [ 5] 9.01-10.01 sec 113 MBytes 944 Mbits/sec - - - - - - - - - - - - - - - - - - - - - - - - - [ ID] Interval Transfer Bitrate [ 5] 0.00-10.01 sec 1.11 GBytes 949 Mbits/sec sender [ 5] 0.00-10.03 sec 1.10 GBytes 945 Mbits/sec receiver iperf Done. ``` </AccordionContent> </AccordionItem> <AccordionItem value='iperf3-reverse-test'> <AccordionTrigger>反向测试</AccordionTrigger> <AccordionContent> ```powershell PS > iperf3 -c 192.168.1.2 -R Connecting to host 192.168.1.2, port 5201 Reverse mode, remote host 192.168.1.2 is sending [ 5] local 192.168.1.1 port 57949 connected to 192.168.1.2 port 5201 [ ID] Interval Transfer Bitrate [ 5] 0.00-1.00 sec 113 MBytes 943 Mbits/sec [ 5] 1.00-2.00 sec 113 MBytes 945 Mbits/sec [ 5] 2.00-3.00 sec 113 MBytes 947 Mbits/sec [ 5] 3.00-4.00 sec 112 MBytes 943 Mbits/sec [ 5] 4.00-5.00 sec 113 MBytes 948 Mbits/sec [ 5] 5.00-6.00 sec 113 MBytes 948 Mbits/sec [ 5] 6.00-7.00 sec 113 MBytes 948 Mbits/sec [ 5] 7.00-8.01 sec 113 MBytes 948 Mbits/sec [ 5] 8.01-9.01 sec 113 MBytes 948 Mbits/sec [ 5] 9.01-10.01 sec 102 MBytes 851 Mbits/sec --- [ ID] Interval Transfer Bitrate [ 5] 0.00-10.01 sec 1.09 GBytes 937 Mbits/sec sender [ 5] 0.00-10.01 sec 1.09 GBytes 937 Mbits/sec receiver iperf Done. ``` </AccordionContent> </AccordionItem> </Accordion> 双向网速都在 936 Mb/s = 117 MB/s 以上,非常完美 🥵,而且不得不说,Wi-Fi 比双绞线复杂太多了,双绞线一插就能近乎满速,Wi-Fi 就 …… ## 推荐软件 - [WiFiman Desktop](https://ui.com/download/app/wifiman-desktop) ## 注意事项 - 路由器不要开 [双频合一](#双频合一与同步双频),前面提到了 - 代理会影响最高速率,例如我代理套餐最高是 25 MB/s,一旦走代理,就会限定在其以下 ## 拓扑图 ```mermaid graph TD P(Redmi K70) T(iPad Pro 2021 11 inch) L(拯救者 R7000P 2021) M4(Mac mini M4) C(H3-2sLite) X(小米 AX3000T) F(斐讯 K2) CCTV(摄像头) G((千兆网络)) G -- "光纤" --> C C -- "CAT-5e" --> X X -. "Wi-Fi" .-> P & T & L X -- "CAT-5e" --> F & M4 X -- "CAT-5e + POE 供电" --> CCTV ```
大家好啊,今天来点大家想看的东西啊。  一人多设备的情况已经很常见了,在此分享一下自己的多设备协同体验。 ## 设备清单 | 设备 | 型号 | 简要备注 | | :--------: | :---------------------: | :---------------------------------------------------------------------------------------------: | | 手机 | [Redmi K70] | 单 USB-C;蓝牙 5.4 | | 平板 | [iPad Pro 2021 11 inch] | 单雷雳 4 可 DP 1.4;蓝牙 5.0 | | ~~Mac~~ | ~~[Mac mini M2]~~ | ~~双雷雳 4 可 DP 1.4;双 USB-A;单 HDMI 2.0;蓝牙 5.3~~ | | Mac | [Mac mini M4] | 正双 USB-C 10 Gb/s;反三雷雳 4 可 DP 1.4;单 HDMI 2.1;蓝牙 5.3 | | 笔记本电脑 | [拯救者 R7000P 2021] | 单 HDMI 2.1;双 USB-C 10 Gb/s 可 DP 1.4,其一 PD 100 W;四 USB-A 5 Gb/s;蓝牙 5.1 | | 蓝牙耳机 | [AirPods Pro II] | 单 USB-C;蓝牙 5.3 | | 显示器 | 泰坦军团 P2SA2V 4K@144 | 单 DP 1.4 双 HDMI 2.1 均 DSC;单 USB-C 可 DP 1.2、PD 65 W,单 USB-B,其一作双 USB-A 5 Gb/s 上行 | | 键盘 | 狼蛛客制化旗舰 F99 系列 | 单 USB-C,回报率 1000 Hz;蓝牙 5.0,回报率 125 Hz;无线 2.4G,回报率 1000 Hz;电池 8000 mAh | | 鼠标 | 罗技 G502 HERO | 按键宏编程;双模式疾速滚轮 | [Redmi K70]: https://www.mi.com/redmi-k70/specs [iPad Pro 2021 11 inch]: https://support.apple.com/zh-cn/111897 [AirPods Pro II]: https://support.apple.com/zh-cn/111834 [Mac mini M2]: https://support.apple.com/zh-cn/111837 [Mac mini M4]: https://support.apple.com/zh-cn/121555 [拯救者 R7000P 2021]: https://item.lenovo.com.cn/product/1013207.html ## 参考信息 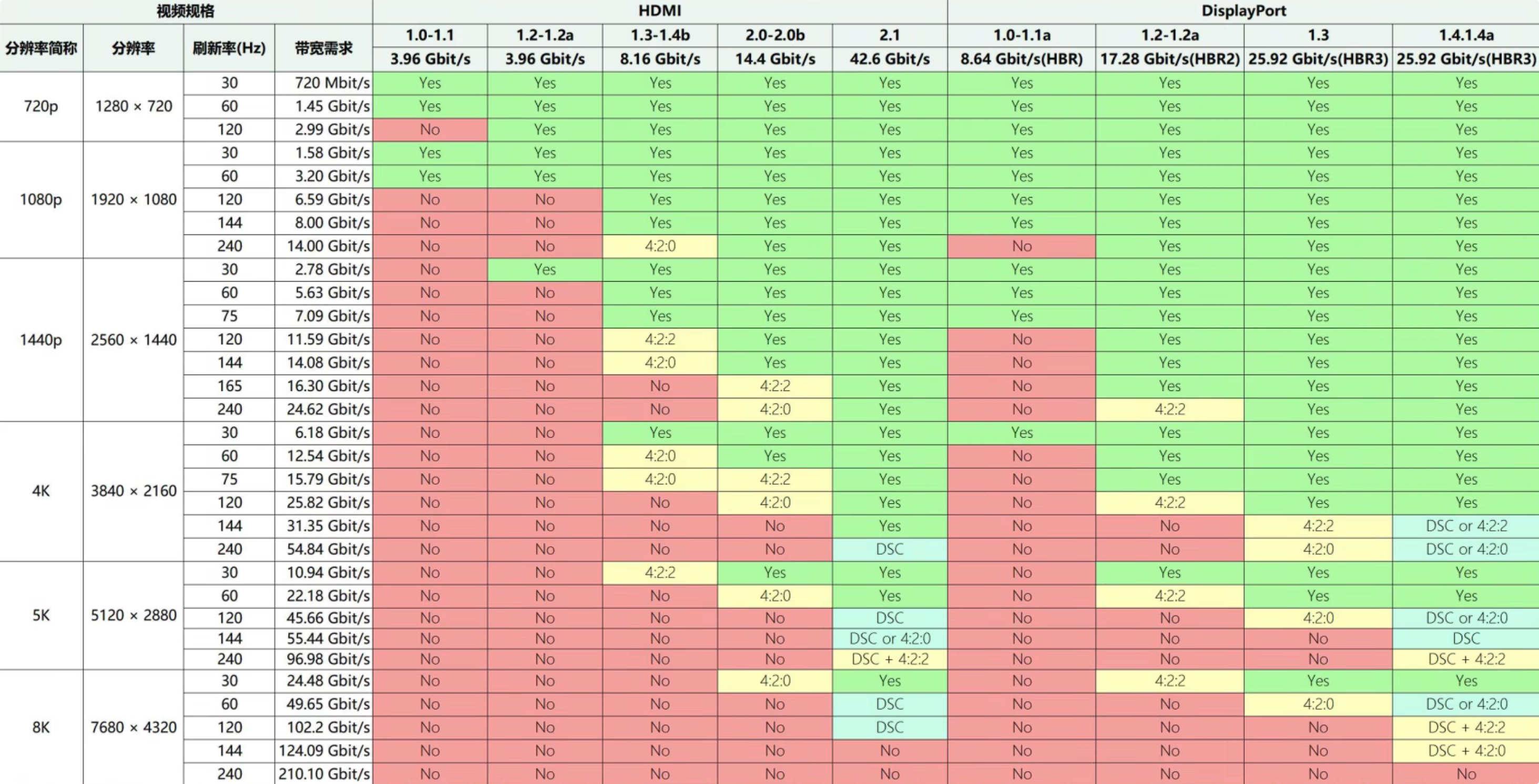 | USB 协议 | 曾用名 | 带宽 | | :----------------: | :-----------------------------------: | :------: | | USB 2.0 Low-Speed | USB 1.0 | 1.5 Mb/s | | USB 2.0 Full-Speed | USB 1.1 | 12 Mb/s | | USB 2.0 High-Speed | USB 2.0 | 480 Mb/s | | USB 5 Gb/s | USB 3.0、USB 3.1 Gen 1、USB 3.2 Gen 1 | 5 Gb/s | | USB 10 Gb/s | USB 3.1、USB 3.1 Gen 2、USB 3.2 Gen 2 | 10 Gb/s | | USB 20 Gb/s | USB 3.2 Gen 2x2 | 20 Gb/s | | USB 40 Gb/s | USB 4 V1.0 | 40 Gb/s | | USB 80 Gb/s | USB 4 V2.0 | 80 Gb/s | | 参数 | 全功能 USB-C | USB 40 Gb/s | USB 80 Gb/s | 雷雳 3 | 雷雳 4 | 雷雳 5 | | :------------: | :----------: | :-----------: | :---------: | :--------: | :--------------------: | :--------------------: | | 带宽 Gb/s | 10 | 40 | 80 | 20/40 | 40 | 80 | | PCIe Gb/s | - | - | - | 16 | 32 | 64 | | 外接显卡 | 不支持 | 可选 | 可选 | 强制 | 强制 | 强制 | | PD 供电 | 可选 100 W | 可选 100 W | 可选 240 W | 可选 100 W | 标配 100 W,可选 140 W | 标配 140 W,可选 240 W | | 反向供电 | 4.5 W+ | 7.5 W+ | 7.5 W+ | 15 W+ | 15 W+ | 15 W+ | | 视频协议 | 可选 DP 1.4 | 可选 DP 2.1 | 可选 DP 2.1 | DP 1.4 | DP 1.4 | DP 2.1 | | 视频传输 | 4K@120 | 4K@240、8K@60 | 双 4K | 双 4K | 双 4K | 双 8K | | USB 4 规范 | 兼容 | 合规 | 合规 | 兼容 | 合规 | 合规 | | Intel DMA 保护 | - | - | - | 可选 | 强制 | 强制 | | 线材认证 | - | - | - | 强制 | 强制 | 强制 | ## 硬件互连 将各个设备用物理连接起来着实废了一番心思。 即便 [USB-C](https://en.wikipedia.org/wiki/USB-C) 能统一接口,各个接口具体支持什么协议也是模糊不清,要在网上搜每个设备的接口支持什么协议,并且还要有能满足这些协议的线材。有够烦人。 总之先讲讲我这套怎么搭的。 ### 共享键鼠 首先将笔记本电脑和显示器用 USB-C 转 [DP](https://en.wikipedia.org/wiki/DisplayPort) 的线连接起来,显示器能以 4K@144 的预期模式显示画面,接着将鼠标和键盘 2.4G 接收器插至显示器 USB-A 口。 问题出现了,照理说这两外设应该连上笔记本电脑的,DP 协议是能够运送双向 USB 信号的 —— 总之再从笔记本电脑连出根 USB-C 转 USB-B 的线,显示器设置使 USB-B 作为上行。 再就是将显示器和 Mac 用双公口 USB-C 的线连接起来,显示器能以 4K@60 的 **惨淡** 模式显示画面 —— 询问客服后得知,显示器的 USB-C 口最高仅支持 4K@60。 不知道为什么,当显示器从 DP 信号源调转至 USB-C 信号源时,USB-C 会夺走 USB-B 上行身份,也就是这根 USB-C 线同时传输了视频信号和 USB 信号。 总之这样键盘和鼠标就能自如的在笔记本电脑和 Mac 之间切换了,更何况键盘还有 Android、Windows、macOS、iOS 四种模式,使用 <KbdGroup><Kbd>Fn</Kbd><span>+</span><Kbd>Q/W/E/R</Kbd></KbdGroup> 快捷键即可切换,非常方便。 ### Mac mini M4 在更换 Mac mini M4 版本后,原先的 HDMI 2.0 接口变成了 HDMI 2.1,那么这个接口就能解决我们之前的问题了,在此使用一根海贝思的支持 8K@60(向下兼容 4K@240)的双 HDMI 公口线将 Mac mini 连接显示器,显示器能以 4K@144 的模式显示画面。 是的,如果使用这根线连接笔记本电脑的话,显示器并不能以 4K@144 的模式显示画面,只能支持到 4K@120,貌似是 [DSC 显示流压缩技术](https://en.wikipedia.org/wiki/Display_Stream_Compression) 并没起作用 …… 虽然说这也是挺高的刷新率了,但我就是希望顶满 144 Hz,因而笔记本电脑和显示器只能用 USB-C 转 DP 的线连接。 此外,显示器在切换信号源时并不会出现“夺走上行身份”这种事,而是显示器为每个信号源各自记忆上行接口,笔记本电脑仍使用 USB-B 作为上行,而 Mac mini 使用 USB-C 作为上行 —— 这里要注意的一点是,与 Mac mini 连接的这根双 USB-C 的线只能是充电线,不能是数据线,否则 Mac mini 既会从 HDMI 2.1 接口输出视频信号,又会从 USB-C 接口输出视频信号,就挺幽默的。 ### 共享音频 在这里点名批评 Mac 的狗屎设计,连接显示器后就不能在状态栏调整音量了,想调只能去按显示器,纯傻逼 —— 据说有人为此就要买 Mac 不买 Windows 设备,因为 Windows 音质是有损的才能随意调音量 —— 巨傻逼,那我缺的这个音量调节谁给我补啊。 总之在试过几款软件后都觉得不尽人意,我就直接禁止 Mac 播放声音了。 对,解决办法是使用 AirPods Pro 无线连接 Mac,这样调节音量就扫扫耳机柄就行,更好的是,AirPods Pro 支持 Apple 设备音频串流,也就是说 Mac 和 iPad 能同时连接至耳机,哪一方有声音就播放哪一方 —— 等一下?为什么不是同时?傻逼 Apple 😅。 而笔记本电脑由于能随意调整音量,所以外放 OK,当然连耳机也行。 再说个有关蓝牙耳机的事,自我开始用 AirPods Pro 我才知道,原来其他设备是能在已有设备与耳机连接时打断连接并连接上的,这应该是蓝牙耳机都有的功能就是了。 多个题外话,Mac 能投屏至 iPad、能鼠标流转操作 iPad(两者意思不同),这个我真觉得很厉害,~~不觉得很酷吗?~~ ## 软件互联 ### 文件传输 非常推荐 [LocalSend](https://github.com/localsend/localsend) 喵!其是基于 Flutter 开发的全平台文件传输软件,只要是在一个局域网下的设备就能互传。 那我为什么不使用 [SMB](https://en.wikipedia.org/wiki/Server_Message_Block) 或 [FTP](https://en.wikipedia.org/wiki/File_Transfer_Protocol) 呢?因为太繁琐了,IP 地址会随着网络环境不同而改变,主机名、用户名、域、密码我还不知道哪个对应哪个,以及各个设备没有一个统一的界面,学习成本高。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2025-01-05T19:11:42+08:00 补充</AlertTitle> <AlertDescription>实际上可以配置路由器以固定 IP</AlertDescription> </Alert> 当然,如果非要使用 FTP 的话推荐软件 [MaterialFiles](https://github.com/zhanghai/MaterialFiles),其之前在 [云盘同步及 Obsidian 相关](/post/Cloud-Drive-Sync-And-Obsidian-Related) 介绍过,能在 Android 设备上启动 FTP 服务器。 ### Android 投屏至电脑 非常推荐 [scrcpy](https://github.com/Genymobile/scrcpy) 喵!其是一款特别厉害的投屏软件,支持有线连接 —— 好像也能无线?因为我第一次用这个的时候感觉它和 [ADB](https://developer.android.com/tools/adb) 挺像的 —— 以及鼠标控制、高刷 …… 具体的不多说了,稍微有点门槛的就是这是个没有 GUI 的软件,当然也可以去找人家包的 GUI。 ## 杂项 ### 桌面自定义 Windows 的可玩性比 macOS 高多了,[Wallpaper Engine](https://store.steampowered.com/app/431960/Wallpaper_Engine) 这玩意要是能有 macOS 版那我会笑醒,接下来大多讲的还是 Windows 方面的东西。 #### 程序坞 macOS 上有程序坞,Windows 有任务栏,但我可不想把程序全“固定到任务栏”,所幸有款名为 [LightFrame](https://lightframe.vertillusion.xyz) 的软件,其有一个组件是 Minecraft 物品栏程序坞,这可真是绝妙的点子,所以狠狠地用 —— 但它也有不足之处:作者不开源,加上年龄较小(?),代码很可能是一坨;存在置底设置经常失效的问题、存在不适配多显示器的问题(把它拖到外接显示器上,以后只用笔记本就看不到了)、存在不响应 [DPI](https://en.wikipedia.org/wiki/Dots_per_inch) 变化的问题 —— 显示器之间拖动大小不发生改变。 最大的问题是,我想在 macOS 上也用它,但是完全不支持。 个人是想在 Flutter 实现无头应用 —— 没有 GUI 也能后台运行的应用 —— 和多视图 —— 支持 0 个及 1 个以上的窗口 —— 后自己实现一个。 #### 鼠标宏 罗技鼠标支持按键宏编程,也就是支持按键映射,而且 Windows 和 macOS 都支持。 | 应用 | 配置 | | :------------: | ---------------------------------------------------------------------------------------------------------- | | Microsoft Edge | 左右推中键能 `返回标签页` 和 `重做标签页`,也就是浏览器历史跳转;拇指上下键能 `重开标签页` 和 `关闭标签页` | | Minecraft | G Shift 键能间隔攻击,对于刷怪塔 AFK 很有帮助 | | VSCode | G Shift 键映射为 F5,方便调试;拇指上下键能 `跳转至上个位置` 和 `跳转至下个位置`,也就是光标位置历史跳转 | 玩法特别多,帮助也很大。 #### 全局工具 在 Windows 上推荐 [PowerToys](https://github.com/microsoft/PowerToys) 的 [PowerToys Run](https://learn.microsoft.com/zh-cn/windows/powertoys/run),macOS 上推荐 [Raycast](https://www.raycast.com)。 使用什么快捷键来呼出快捷栏呢?在 Windows 上我是 <KbdGroup><Kbd>Ctrl</Kbd><span>+</span><Kbd>Win</Kbd><span>+</span><Kbd>Alt</Kbd><span>+</span><Kbd>␣</Kbd></KbdGroup>,在 macOS 上 …… 我哪知道,macOS 的键位好奇怪,我键盘切换到 macOS 模式后把 <Kbd>Win</Kbd> 和 <Kbd>Alt</Kbd> 互调了,然后我又在 macOS 设置里将 <Kbd>Command</Kbd> 和 <Kbd>Ctrl</Kbd> 对调了,这样才使得 macOS 的键位和 Windows 一致。  在此,macOS 上的要做的更好,扩展多 —— 翻译、词典、ChatGPT 对话等等,不过有些功能要订阅制付费 —— 能给每个功能自定义全局快捷键,界面还挺舒适 —— 相比之下 Windows 一开始的样式丑的我根本不想用 —— 补足了很多 macOS 本应该有的功能。 如:Windows 上 <KbdGroup><Kbd>Win</Kbd><span>+</span><Kbd>V</Kbd></KbdGroup> 的剪切板,QQ 提供的 <KbdGroup><Kbd>Ctrl</Kbd><span>+</span><Kbd>Alt</Kbd><span>+</span><Kbd>A</Kbd></KbdGroup> 截图功能,Windows 上的 Everything 全局搜索功能。 对了,讲讲 [Everything](https://www.voidtools.com/support/everything),这是 Windows 上很强力的一款全局搜索软件,能秒搜出结果,还支持正则表达式。 在它的最新版本 `1.5a (1.5.0.1366a)` 还支持了暗色模式,纯属鉴作! #### 更好的 Windows 11 更好的 Windows 11 就是 Windows 10,Windows 11 有些地方真的不如 Windows 10,那么 [ExplorerPatcher](https://github.com/valinet/ExplorerPatcher) 就是把 Windows 11 改造的更像 Windows 10 的一个工具,部分功能如下: - 自由切换 Win 10 和 Win 11 任务栏,支持设置标签合并、功能显示等。 - 恢复 Win 10 右键菜单和文件管理器命令栏。 - 切换开始菜单版本、禁用推荐、自动打开所有应用页面。 - 自定义应用切换器,可选 Win 11、Win 10、Win NT 等风格。 😤 微软,你好好看开发者怎么教你做事 😤 ### 其他 更多的见 [此 GitHub 仓库](https://github.com/Cierra-Runis/desktop_modified),里面分享了更多自定义工具。 ## 拓扑图 ```mermaid flowchart TD P("Redmi K70") T("iPad Pro 2021 11 inch") L("拯救者 R7000P 2021") M4("Mac mini M4") A("AirPods Pro II") D("泰坦军团 P2SA2V 4K@144") K("狼蛛客制化旗舰 F99") M("罗技 G502 HERO") L -- "USB-C 转 DP" --> D L -- "USB-C 转 USB-B" --> D M4 -- "HDMI 2.1" --> D M4 -- "USB-C" --> D D -. "USB-A 2.4G 接收器" .-> K D -- "USB-A" --> M P & T & L & M4 -. "蓝牙" .-> A ```
本篇博客是本人给 MIT 课程《计算机教育中缺失的一课》写的一些笔记和个人感悟,不作为课程的代替。 在此附上 [中文讲义](https://missing-semester-cn.github.io) 和 [bilibili 熟肉](https://www.bilibili.com/video/BV1b2421M7v3)。 ## 路径 路径这个应该是比较基础的东西了,`.` 代表当前目录,`..` 代表上一级目录,这些在 Windows 里也是相通的。 但 Windows 和 Unix 系统的路径分隔符是不同的,Windows 使用 `\`,而 Unix 使用 `/`,所以我们最好使用一些库来处理路径,如 Python 的 `os.path`,自己处理路径容易出现问题。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2025-01-11 14:25:09 提醒</AlertTitle> <AlertDescription> Python 的 `os.path` 已经逐渐被推荐用 `pathlib` 替代,更现代化,也更易读 </AlertDescription> </Alert> 令我印象比较深刻的是 [LeetCode 71 题](https://leetcode.com/problems/simplify-path),其要求简化一个 Unix 风格的路径,非常推荐大家去做一下。 ## Shell 与 Bash 这一节内容实际上在 [SSH](/post/SSH) 中已经提到了,这里再补充一些。 实际上我在以前都是使用 Python 来写脚本的,比如 Mercurius 用于构建 APK、Windows ZIP 并将它们移动到 `out` 文件夹的脚本,而这实际上要求使用脚本的人都安装了 Python,这显然不是一个好的选择。 而 Bash 是 Unix 系统的默认 Shell,其脚本文件以 `.sh` 结尾,而在 Windows 上,我们可以使用 WSL 来运行 Bash 脚本 —— 当然我觉得 Windows 上应该还得是使用 PowerShell,其脚本文件以 `.ps1` 结尾,当然还有 `.bat` 和 `.cmd` 这种比较古老的批处理文件。 在看本节课的同时,我也在使用 Termux。由于 GitHub 最近抽风,完全看不到最近有哪些仓库有新的 Release,于是结合 `GitHub CLI` 和 `jq` 命令,我写了一个脚本来获取最近的 Release,在此就不献丑了。 ## Regex 正则表达式是一种用于匹配字符串的模式,其在很多地方都有应用,如搜索引擎、文本编辑器、IDE 等。 在我刚学习 Java 的时候,写了一个模拟 Minecraft 命令的 Java 程序,我使用的还是字符串切割: ```java // 匹配指令 public void match(String input) { int i; // 指令索引 for (i = 0; i < Command.length; i++) { // 搜索 // 若输入的指令左边部分与指令库中指令相符 if (input.regionMatches(0, Command[i], 0, Command[i].length())) { // 则将左边部分切掉,把指令索引和右边切片传入 toCommand 函数 input = input.substring(Command[i].length()); String[] splitCommand = input.split(" "); // 以空格切分输入的命令 toCommand(i, splitCommand); return; } } // 否则提示无匹配指令 if (i == Command.length) { System.out.print("\33[31;1mNo matched command!\33[0m\n\n"); } } ``` 如果使用正则表达式,那么这个程序可能会更加简洁 —— 当然,像这种命令行程序都是有对应的包的,如 [Picocli](https://github.com/remkop/picocli)、[JCommander](https://github.com/cbeust/jcommander) 以及 Kotlin Only 的 [Clikt](https://ajalt.github.io/clikt) 等。 后来发现,VSCode 也支持正则表达式,自己也在写 Python 爬虫时用正则表达式来清洗出想要的内容,到现在 [Mercurius](https://github.com/Cierra-Runis/mercurius) 也支持使用正则表达式搜索日记内容,不得不说正则表达式非常强大。 但正则表达式有时也有一些坑,比如 [「熟肉」非常慢代码来自 Cloudflare, 使整个公司瘫痪](https://www.bilibili.com/video/av1350874531) 这个视频,一个小小的 `.*.*=.*{:regex}` 的正则表达式干烂了整个 Cloudflare。 ## Vim 我目前还是使用 VSCode 的啦,让我完全转向 Vim 还是挺困难的: 1. Vim 的上手难度高 2. Vim 跑在 Shell 里,那我一些实时预览的内容,如 PDF、网页、APP 该如何操作? 丢掉鼠标还是不那么现实的,但我确实想加快自己的编程速度,可能 VSCode 的 Vim 插件能帮忙? 但这和真正的 Vim 又会有多大的区别呢?是否需要先学习 Vim 在使用 Vim 插件呢? ## 语义化版本号 语义化版本号参见 [此链接](https://semver.org)。 我最早认识到版本号应该还是 Minecraft 的版本号,如 `1.7.2` 这样的,但 Minecraft 并不完全遵循这一规范,而在 Snapshot 快照版本号上我们还能见到另外一种版本号格式:`24w06a`,其 `24` 代表 2024 年,`w06` 代表 6 周,`a` 代表这一周的第一个快照版本。 其具体格式参见 [此链接](https://minecraft.wiki/w/Version_formats)。 ## `source script.sh` 和 `./script.sh` 的区别 我隐约记得前者被称作源化,第一次使用这个命令则是在配置 zsh 的时候。 具体来说,前者是在当前会话运行 sh 文件,如果在文件内进行了如环境变量的配置,那么运行之后这个配置则会应用到当前会话;而后者则是在一个子进程中运行,其不会影响至外部的会话。 除此之外,后者还要求用户对其拥有运行权限,需要使用 `chmod +x script.sh{:bash}`。 ## 个人想法 如果说这是“计算机教育中缺失的一课”,那么我缺失的可就不止一课了。 我能说这节课包含了绝大多数这几年自己了解的课堂外的知识,而这些知识相比于 408 那四大样 —— 虽然说它们也是不能忽视的 —— 是更加符合实践的。我反正不会成天去搞数据结构、计算机组成原理、计算机网络、操作系统这些东西。 我觉得兴趣也是很重要的,那四大件的教学模式,完全就是空中楼阁,让人完全提不起兴趣 —— 然而前段时间了解 GFW 的一些原理时不是看的很开心吗? 同时我还是发现自己学的东西太少了,知识面就算较广,其深度也没达到令人满意的地步,所以趁现在还有半年毕业的时间里,我会多看些这样的公开课。
[Git](https://git-scm.com) 的基础安装不在此赘述,在此记叙些 Git 相关的其它知识。 ## 使用 GPG 签名 在基础安装后,其实我们还能做一些有趣的事情 —— 对于我来说,是注意到 Git 提交记录中 `未验证` 的橙色 Badge 而感兴趣的 —— 就是使用 GPG 来给我们的提交签名 —— 从而使 Badge 变成绿色的 `已验证`。 其实我在时间上是更早就在 Git 中使用了 GPG 签名,而 [SSH](/post/SSH) 是更晚接触的,照理,他们可以使用同一套 GPG 公私钥,我应该会在以后统一为一个密钥。 配置方法略,还请自行搜索。 ## 使用简洁、明确的标题与约定俗成的提交类型 - 每个提交信息应以一个简短的动词(通常是过去式)开始,描述这次提交的主要修改 - 标题应简洁明了,尽量不超过 50 个字符 - 标题后不要加句号 `.` 示例: - `feat`: 新功能 - `fix`: 修复 bug - `docs`: 文档更新 - `style`: 代码格式 - `refactor`: 代码重构 - `test`: 测试 - `chore`: 杂项 - `fix: Fix Login Button Alignment` - `feat: Add User Model` ```plaintext refactor: Extract Authentication Logic into Middleware This makes the authentication logic reusable across multiple routes and reduces duplication of code. ``` 标题大小写的主要规则如下: - 首字母大写:标题的第一个和最后一个单词必须大写,无论词性 - 实词大写:名词、代词、动词、形容词、副词等都大写 - 虚词小写:冠词(a, an, the)、连词(and, or, but)、介词(in, on, at, etc.)等通常小写,除非它是标题的第一个或最后一个单词 ## 使用小而频繁的提交 避免一次写很多功能,专注于一处,每个提交解决一个问题或完成一个功能。这有助于代码的审查、回滚和后期维护。 ## 避免 WIP 提交 如果提交不完整,应该避免推送到主分支。可以使用 `git commit --amend{:bash}` 来修改最后一次提交,其用法和注意事项如下: 1. 修改提交消息 ```bash git commit --amend ``` 2. 添加忘提交的文件 ```bash git add <missing_file> git commit --amend ``` 3. 移除误提交的文件 ```bash git rm --cached <wrong_file> git commit --amend ``` <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>影响提交历史</AlertTitle> <AlertDescription> 使用 `--amend` 会改变提交的哈希值,若提交已经被推送到远程仓库,则修改提交后需要强制推送。这可能影响其他协作者的工作,需要慎用。 </AlertDescription> </Alert>
咳咳,本博客已经转向 Next.js,足以证明 Next.js 框架的先进(自卖自夸)。 遗憾的是至今都没有对 Vue 感兴趣,所以本期使用报告并不会有那样的对比,但还是有别的内容的。 ## Vercel 之前自己的博客是搭建在 [GitHub Pages](https://pages.github.com) 上的,而 GitHub Pages 是一个静态网页托管平台,这说明网页的内容是静态的,这很适合博客这一类更新频率低,不需要用户登录交互的场景。 这次转向 [Vercel](https://vercel.com) 单纯是因为其对 Next.js 有很好的支持 —— 因为 Vercel 就是搞 Next.js 的那群人做出来的。 可玩性比 GitHub Pages 要高多了,不局限于原先的 [Hexo 框架](https://hexo.io) 和 [Butterfly 主题](https://butterfly.js.org),任何地方都能自己去设计。 Vercel 还提供了 [Analytics](https://vercel.com/docs/analytics) 和 [Speed Insight](https://vercel.com/docs/speed-insights) 功能,可以查看网页状态,开箱即用非常方便。 其实之前也想用 GitHub Actions 来监视仓库变化,以自动构建、部署网页,但总之还是麻烦的,后面不了了之。而 Vercel 在链接到 GitHub 仓库后就能自动 CI/CD,极度方便线上做一些简单的改变 —— 用 GitHub 客户端写个 [MDX](https://mdxjs.com) 的事。 ## International 国际化一直是我很喜欢做的一件事,[Mercurius](https://github.com/Cierra-Runis/mercurius) 就实现了 en、zh-CN、ja 三种语言,我也想博客支持多语言。 国际化的资料还是比较少,直到 Next.js 15 才内置了这个功能(存疑)—— 虽然说在此之前我也不知道国际化是个什么情况就是了。 其实我一度想用 [Docusaurus](https://docusaurus.io) 来搭建博客,但正如前面提到的,不想被某个框架局限,最终还是决定自己搭建。 但这也带来了一个问题,该如何对 MDX 内容进行国际化?目前我还没有想到一个好方法。 ## 字体 前面的国际化同样会带来一个问题,如何对字体进行国际化。要知道汉字在不同的国家和地区会有不同的字形 …… 总之先摸鱼了,优先度比较低的 Issue 总是这样,被忽略,被拖延 …… ## NextUI 我很喜欢 [NextUI](https://nextui.org) 这个 UI 库,其更新频度挺高的,可惜目前我重写博客的时机好像有点不太好,卡在 Next.js 14 到 15、[Tailwind CSS](https://tailwindcss.com) 从 v3 到 v4、NextUI 更新 v2.6 版本、ESLint 结束 v8.x 版本维护的这个时间点,许多从网上找的教程还是基于老版本的,也就带来了不便。 好像有点偏题了,说回 UI。 我不会设计颜色,或者说我想要使用的颜色很难去找到一个好看的色盘: 就以彩虹上出现的七种颜色来说,红色用于 Error,橙色用于 Warning,绿色用于 Success,蓝色用于 Primary,紫色用于 Secondary。但我一旦想把橙色作为 Primary,一下就很难设计一个好看、直观的色盘了。 对于背景色,我直接抄的 [One Dark Pro](https://binaryify.github.io/OneDark-Pro) 的颜色,这真的好看吧。 还有一点,我已经很久没使用亮色模式了,所以对于设计出的亮色模式下的配色,我是极度的感到不适应 …… 其实博客只想支持暗色模式的,但 ~~挑战自己,逆境翻盘~~ 这就当作是学习了 —— 实际上还不应该拘泥于 light 和 dark 两种模式,多主题不是更好? ## 包管理器 目前我使用的是 [yarn v4](https://yarnpkg.com) 版本,目前我还是挺喜欢这个包管理器的,但像是 [pnpm](https://pnpm.io)、[bun](https://bun.sh) 我也非常想尝试,什么时候会转向 pnpm 或者 bun 也说不定,特别是 bun,一个挺厉害的 JavaScript 运行时,还加了很多好东西 …… 但我之前在 Windows 安装后升级出了一点问题来着,也就暂时搁置了。 ## 总结 Next.js 确实是很不错的网页前端框架,别急,与 Vue 的对比总会来的,实际上,我已经对 Vue 有一点看法了,按下不表喵。
## 奔向命令行 大家第一次使用命令行或见到终端是什么时候呢?大多是第一次编写 C 语言程序吧。 我是小学用 `bat` 文件开 Minecraft 服务器时接触的,当时就想这个界面可真丑,黑咕隆咚的 —— 现在不一样了,尽情美化喵。 终端是展示 Shell 的窗口,而 Shell 的话,Windows 有 [cmd](https://learn.microsoft.com/en-us/windows-server/administration/windows-commands/cmd)、[PowerShell](https://github.com/PowerShell/PowerShell)、[Windows PowerShell](https://learn.microsoft.com/en-us/powershell/scripting/what-is-windows-powershell),macOS、Linux 有 [Bash](https://www.gnu.org/software/bash),Android 可以使用 [Termux](https://github.com/termux/termux-app),也相当于是 Linux 了 —— 有关 Termux 的配置详见 [Termux 高级终端安装使用配置教程](https://www.sqlsec.com/2018/05/termux.html)。 macOS 和 Linux 的关系更近,总之都能使用 [Zsh](https://ohmyz.sh) 而不是 Bash 作为 Shell,有关 Zsh 的配置参见 [这篇文章](https://www.mintimate.cn/2021/02/05/configZsh)。 Zsh 相比 Bash 能提供命令行历史补全的功能,在 Windows 上,这需要下载 [PowerToys](https://github.com/microsoft/PowerToys) 并启用里面的 `未找到命令` 功能 —— 看起来命令行补全是 PowerShell 的功能,但总之这样配置之后就没问题。 在 macOS 上,自带的终端并没有那么“好看”,总之转用了 [iTerm2](https://iterm2.com),相关的配置略。 ## 奔向 SSH 在购入了 Mac mini 后,除了写 [SwiftUI](https://developer.apple.com/xcode/swiftui) 外,也想用 Mac mini 做些别的什么 —— 我是用不来 macOS,操作逻辑相比 Windows 总是有太多别扭的地方,我是应该还会把 Windows 作为主要的开发环境的。 于是看视频,了解到 Mac mini 可以作为 [软路由](https://bulianglin.com/archives/openwrt.html)、[NAS](https://en.wikipedia.org/wiki/Network-attached_storage)、服务器 …… 诶,服务器。 正好最近在玩 Minecraft,而 Mac mini 完全适合 Minecraft 开服 —— 其实就是我想试试看,总之能分担一下我这台 Windows 笔记本的压力吧,让 Mac mini 专心逻辑处理,Windows 笔记本专心渲染。 这就牵扯到远程操作了 —— 这其实不算“远程”,只在内网操作嘛,但 —— 我曾经发病莫名其妙的购买阿里云的服务器,完全不了解自己为什么要用、该怎么去用服务器,总之我确实对 [SSH](https://en.wikipedia.org/wiki/Secure_Shell) 连接这一步有印象。 具体开启 SSH 的流程就不在此赘述了,现在再来谈个别的事。 SSH 支持免密登录,总之使用 [GPG](https://gnupg.org) 的非对称加密 —— 我其实对椭圆曲线的数学性质特别感兴趣,但目前找到的一些资料都是用到了抽象代数的方法的那种,没有传统解析几何的那种解释。 > 加密:公钥加密,私钥解密 > > 公钥公开,任何公钥持有者都可以将想要发送给私钥持有者的信息进行加密后发送,这个信息只有私钥持有者能解密。 > > 签名:私钥加密,公钥解密 > > 公钥公开,任何持有公钥的人都能解密私钥加密过的密文,这个过程并不能保证消息的安全性,但是它却能保证消息来源的准确性和不可否认性,也就是说,如果使用公钥能正常解密某一个密文,那么就能证明这段密文一定是由私钥持有者发布的,而不是其他第三方发布的,并且私钥持有者不能否认他曾经发布过该消息。 ## 奔向 PowerShell 配置好 Windows 和 macOS 上的 SSH 服务后,成功使用 Windows 远程连接到 macOS,相对应的,macOS 也可以远程连接到 Windows,但是远程连接后默认进入的 Shell 居然是 cmd,这个实在是有点搞笑了。 - [SSH 连接 Windows 默认启用 PowerShell](https://learn.microsoft.com/zh-cn/windows-server/administration/OpenSSH/openssh-server-configuration#configuring-the-default-shell-for-openssh-in-windows) - [WSL 默认目录](https://whlit.github.io/linux/wsl-default-dir.html) 如上配置好后,尽情使用 SSH 带来的便利吧。 ## BUG 是的,从 Windows 访问 macOS 使用 `ls/ll` 命令列出含有中文文件的文件夹内容时,会有如下的乱码: ```bash ➜ mods git:(main) ✗ ll total 80440 -rw-r--r-- 1 cierra_runis staff 2.0M Oct 28 04:33 ???Fabric API???fabric-api-0.92.2+1.20.1.jar -rw-r--r-- 1 cierra_runis staff 6.3M Oct 28 04:50 ???Kotlin ?????????fabric-language-kotlin-1.9.5+kotlin.1.8.22.jar -rw-r--r-- 1 cierra_runis staff 533K Oct 28 05:15 ???Masa ????????????malilib-fabric-1.20.1-0.16.3.jar ... ``` 答案是去 `.zsh_rc` 里取消如下的注释,使 `LANG` 得以固定为 `en_US.UTF-8`: ```bash # You may need to manually set your language environment export LANG=en_US.UTF-8 ```
最近在折腾 Minecraft 服务器,有了想写的东西,也就一并写在这里。 ## Minecraft Java Edition 这真的是对我影响最大的游戏,没有之一了。可惜的是,我已经完全没有自己接触的这款游戏时的任何记忆了,想讲的事情很多。 当时玩的最多的单人版本还是 `1.7.2`,其他的比如 `1.6.4`、`1.7.10`、`1.8`、`1.10.2` 这几个比较有记忆点的版本相比之下玩得比较少。而服务器的话,就看服务器是用的哪个版本。 电脑上用的是一款名为“麦块我的世界盒子”的软件,当时我完全没学过 Java,只知道 Minecraft 是用 Java 编写的,不知道 Minecraft 本身不能像 EXE 程序一样双击启动,而是需要启动器启动。启动器也就是包了一层 GUI,方便配置一些启动参数,最后也是一条命令行启动 —— 也是,EXE 是 Windows 系统的可执行文件,而 Minecraft Java Edition 又不是只支持 Windows 的,macOS 和 Linux 都行。~~真的有人会在 Linux 玩游戏吗?~~ 现在比较流行的有 [HMCL](https://github.com/HMCL-dev/HMCL) 和 [PCL2](https://github.com/Hex-Dragon/PCL2) 两款启动器,和麦块一样,只是麦块还带有一些论坛性质,记得还能在上面看相关视频来着。 实际上 Minecraft 是付费游戏,但官方对于盗版的态度很平和,没有进行打压,这也让不少像我这样没有钱买游戏的小朋友玩到它。对于盗版行为,我在以后会写篇文章议论一下。我当时确实很想获取正版账号,因为盗版账号是没有皮肤的,默认为 Steve;以及部分服务器开启了“正版验证”,即只允许有正版账号的玩家加入。 当时的价格为 165 人民币,我是实在都不可能搞到这么多钱,更何况网购还卡脖子,直到初三后才有了网购能力。而 2022 年 5 月 13 日,鉴于 Minecraft 买基岩版送 Java 且价格非常实惠,也就终于入正了,作为这么多年来陪伴的感谢。 在没有正版账号的时候,皮肤可以用皮肤站进行修改,像是现在都还在运营的 [LittleSkin](https://littleskin.cn),而具体的皮肤文件,则可以到 [McBBS](https://www.mcbbs.co) 或是 [我的世界中文下载站](http://www.minecraftxz.com) 找喜欢的,当然也可以自己制作。我自己是不会画的,我找了一个自己喜欢的皮肤,浅浅的修改一下,便有了使用至今的这个皮肤。 [在铁路上](https://zh.minecraft.wiki/w/Tutorial:%E6%88%90%E5%B0%B1%E6%8C%87%E5%8D%97#-{zh-cn:%E5%9C%A8%E9%93%81%E8%B7%AF%E4%B8%8A;zh-tw:%E6%9A%A2%E8%A1%8C%E7%84%A1%E9%98%BB;zh-hk:%E6%9A%A2%E8%A1%8C%E7%84%A1%E9%98%BB;}-) 是 Minecraft 中的一个 [成就](https://zh.minecraft.wiki/w/%E6%88%90%E5%B0%B1%EF%BC%88%E6%B6%88%E6%AD%A7%E4%B9%89%EF%BC%89),它要求玩家“通过矿车旅行,移动到至少离出发点 500 米的位置”,然而不知道为什么,我就是无法获得这个成就 —— 为此还铺设了很长很长的一条轨道,消失在无穷远点的那种 —— 现在想想,可能是创造模式不能获取成就吧。 ## Minecraft Bedrock Edition 手机上用的就是“多玩我的世界盒子”啦,当时里面的很多视频都是转载自 Youtube 的,像是粉红羊、钻石哥啥的。 这里提两个视频。第一个严谨来说是系列视频,官方名称叫 [Minecraft for Noobs](https://youtube.com/playlist?list=PLjxIP-vsTvu3Xg6zWYVNB_urX6dXoI3nY),是个动画视频,推荐看看。第 10 集用到了 [OMFG-Hello](https://www.youtube.com/watch?v=ih2xubMaZWI) 这首歌,总之挺好听的(现在觉得有点土就是了)。 其次是 ## 服务器 /// TODO: 玩服务器 后面开始自己搭建服务器。第一次写 `bat` 文件,面对黑窟窟的 `cmd` 和一堆 log,着实让我头大。 当初选的是 [Sponge](https://spongepowered.org) 端 —— 官网说今年 10 周年,看来这是 2014 年之后的事 —— 教程按 McBBS 来的,现在看来 Sponge 端不温不火的,我现在应该是不会再选这个端了 —— 不一定呢,或许哪天起兴致了会把所有端都体验一次呢。 Sponge 端用的是 plugin 而不是传统的 mod,当初应该是放在 `mods` 文件夹下就是了,现在是 `plugins` 文件夹。这也使得 Sponge 成为了一个比较特殊的端。 ## 再出发
现在的话,大致能写点东西了。 ## 飞机 我认知里的交通工具里,最有技术含量的就是飞机,其次是地铁。地铁有幸在小时候就体验过了,飞机则一直没有乘坐 —— 因为我确乎没有这样的需求,家里人就算行程较远也会选择长途汽车,再就是也从来没有出国旅游、工作、学习。 这次游学之前,有接触到 [ACI](https://space.bilibili.com/358422)(Air Crash Investigation,空中浩劫)这部系列纪录片,讲空难的,也就对飞机感兴趣了。 这次来日本,是先飞到上海再飞到日本的。先到昌北机场把行李托运后给了登机牌,等到登机就上去咯。 这段机程确实没什么餐食,单单给了一个小红豆面包,找到自己位置后做到了靠窗的座位,这样正好可以看着窗外。但这排三个位子只有我一个人,确乎有点害怕。 飞机缓慢(?)地滑行到起飞滑道,然后停住。照纪录片,这里开始确认检查清单。然后便是和滑行时完全不同感觉的加速,加速,[rotate](<https://en.wikipedia.org/wiki/Rotation_(aeronautics)>),起飞。那时候感觉自己就像坐在一个无轨过山车上,一直向上冲刺。 到新的“重力加速度”稳定下来,不依赖窗外的天际线,不仔细观察,确乎很难发现飞机的姿态是向上的。着实稍微理解了什么是空间迷向。 耳压确实能感到变化,但“打开咽鼓管”这种事情我小时候就会了,简简单单就平衡了耳压 —— 据说为了防止机体膨胀回缩造成疲劳,延长飞机的寿命,机内的压强是尽可能低的,低到人体开始感觉异常的临界点。 ## 生活 ### 住 ### 食 一般都会在便利店或自动贩卖机买饮料,有纯净水、咖啡、可乐、麦茶等,但大多数看下来,除了很明显会是甜的东西外,它们大多都是无糖、低糖的。无糖一坨。低糖依托。 自己这次喝到了《命运石之门》里捏他的饮料 [Dr Pepper](https://en.wikipedia.org/wiki/Dr_Pepper),味道,非常,独特。第一次喝还真有点不适应,但味道非常上头,倒是挺喜欢喝。 再就是吃饭。很大的感受就是,咸。我曾多次别扭的表达自己想少放点盐,但我用“少し”而不是“少なめ”,动词变形这块纯纯没学过。此外倒是没有什么,都挺好吃的。就是价格有点贵 …… 对了,杏仁豆腐。杏仁的味道,怪!但好吃。但有次傻逼日本人给了我一袋绿绿的东西,我以为是抹茶什么的,结果是芥末。虽然这只加一点点不是很辣,但我真的有被恶心到。 芥末,我这辈子都吃不来。记得是高中?有同学带了条芥末,试了一点点,那种恶心的、化学刺激性药物的味道,完全不像是辣味了。当时我以为这是什么整蛊专用食品啥的,谁知道真的芥末就这个味。难以忘怀了。 ### 行 日本的交通以电车(地铁?轻轨?火车?)为主,我们从成田机场拿着发的切符(きっぷ)中途有换乘地乘到锦系町(きんしちょう)。 相比国内,日本电车里的广告很多,查看站台信息的地方少。日本电车的运行噪声比国内大,平稳度也没国内好。电车里会看到有人看书,虽然说多数还是会看手机。对了,有关书籍的开本后面我们再谈谈。 一开始我们用的是纸质票,后面也有说给我们统一办 [Suica](https://www.jreast.co.jp/suica) 卡什么的,但总之拒绝了,明明可以自己搞的东西。我自己办了一张 Suica 的实体卡,这卡不仅能用在乘车,还能用在售货机,虽然不是很懂为什么要支持这种功能就是了。 ## 项目 在此不讲项目本身,而讲别的。 ### 时区 在参加项目时,遇到了因中国日本时区不同导致的问题。在此记录与时区相关的信息。 有关 [GMT](https://en.m.wikipedia.org/wiki/Greenwich_Mean_Time)、[UTC](https://en.m.wikipedia.org/wiki/Coordinated_Universal_Time) 的介绍参见其链接。 简而言之,现在开始我会尽可能使用 [ISO 8601](https://en.m.wikipedia.org/wiki/ISO_8601) 表示时间。 使用 [时间戳](https://en.m.wikipedia.org/wiki/Timestamp) 是不好的: 1. 标准上其表示整秒数,精度低 —— ISO 8061 支持秒数带有小数 2. 有些情况毫秒数 Millisecond 和微秒 Microsecond 也被运用,就我曾保存过的一张照片其文件名就是以毫秒数保存的 3. 32 位系统下会引发 [2038 年问题](https://en.m.wikipedia.org/wiki/Year_2038_problem) 4. 人类不可读
不想说好话,因为鸿蒙 ArkUI 就是纯纯的一坨。 给目前自己接触过的大前端框架拍个名的话: | 名次 | 框架 | 备注 | | :--: | :-------------: | :------------------------------------------------------: | | 1 | Flutter | 当之无愧 | | 2 | SwiftUI | 除了文档没有示例,代码格式化不舒服外,框架本身是没问题的 | | 3 | Next.js | 前端的神 | | 4 | Electron | 桌面端的神,但我不喜欢什么东西都是浏览器套壳 | | 5 | React Native | 页面路由麻烦,开发工具不方便 | | 6 | Jetpack Compose | 半成品 | | 7 | ArkUI | 残次品 | 它的 IDE 弱智到什么程度呢?连最起码的变量类型都显示不对,Linter 诡异莫测完全不起作用,代码补全完全残废,连 Code Fix 也没有。 有人真要是能对这坨东西骄傲的说有多么厉害那还是屎吃多了不知道饭是咋样的。 状态管理是抄都抄不懂啊!就连最简单的父组件的给子组件传参,父组件的状态变化了不影响子组件,要多在子组件参数加上 `@Link{:ts}` 注解,那这样我要是子组件有很多参数依赖是不是得把参数都加上 `@Link{:ts}` 注解?那如此的话模板代码量不就又上去了? 完全不看好 ArkUI 未来的发展,希望早日暴毙。
大家好啊,今天来点大家不想看的东西啊。 ## ArkTS 语言 > [ArkTS](https://developer.huawei.com/consumer/cn/arkts) 是鸿蒙生态的应用开发语言。 > > 它在保持 [TypeScript](https://www.typescriptlang.org) 基本语法风格的基础上,进一步通过规范强化静态检查和分析,使得在程序运行之前的开发期能检测更多错误,提升代码健壮性,并实现更好的运行性能。 > > 同时,提供了声明式 UI 范式、状态管理支持等相应的能力,让开发者可以以更简洁、更自然的方式开发高性能应用。 官网是这样说的,但我只能呃呃。可能是华为没有那样的能力去创建一门属于自己的语言吧,最后把 TypeScript 变成了与 Swift 或者说是 Kotlin 缝合的缝合怪。一些令我厌烦的写法,如匿名函数 `.bind(this){:ts}`、模板字符串要用反引号 ``const str = `Show: ${another} value`{:ts}``,也遗传了下来,特别是组件内引用 `state{:ts}` 时也要带上 `this{:ts}`,这肯定是受到语言实现的限制吧。 同样的,我不喜欢 ArkTS: 1. 必须使用 DevEco Studio 才能使用 ArkTS 语言 2. DevEco Studio 自带的代码格式化结果一坨: ```ts .toolBar({ items: [ { value: "Plunger", icon: "house", action: () => { } }, { value: "Intelligent", icon: "house", action: () => { } }, { value: "Shop", icon: "house", action: () => { } }, { value: "Me", icon: "house", action: () => { } }, ] }) ``` 真看不下去吧,这都和 Xcode 学一样? 3. 格式化风格不统一,和 Swift 一样,加几个回车和空格格式化结果就不一样了,多人协同我不敢想会是怎么样的 4. 没有热更新,但和 SwiftUI 一样提供了 `Preview` 功能 —— 因为如果连 `Preview` 功能都没有的话,对于连模拟器都不支持的 DevEco Studio 来说,没有鸿蒙设备就别想搞鸿蒙开发了 ## DevEco Studio 我去,这不是我们 Android Studio 吗,啊不对,这不是我们 IntelliJ IDEA 吗?下次发布记得标注。 其实就是没能力自研 IDE 啦,所以选择“基于 IntelliJ IDEA Community 开源版本打造”。这个选择是正确的,但结果只能说不尽人意。 首先是代码格式化的问题,这个上面讲过了,那么接下来说点别的。 插件未免太少了,因为自己最常用的代码编辑器是 VSCode 嘛 —— 其实在我心目中这玩意可以说是和 IDE 一样的存在了 —— 所以键位肯定也想按 VSCode 的来,在 IntelliJ IDEA 和 Android Studio 上都有 VSCode KeyMap 的插件可以从 VSCode 导入键位,但 Dev Studio 上就是没有。 难道说华为就完全没有在使用 VSCode 的吗 …… 我去,Xcode 也没有,这下破案了。 代码补全一坨,这是做的极差的。感觉代码补全完全没有根据上下文,也就是光标目前所处的地方该填什么类型的东西、默认能填什么东西,来提示补全内容 —— 原版 TypeScript 在 VSCode 上的代码补全可谓是反向的极端,过度依赖上下文以至于有时我想要的结果反而不在补全结果里。 本地化做的不到位,照理说这还是国内公司的软件本地化应该做的更好,但很多地方都没有翻译到 —— 有人可能会说全英文界面更好,开发者就应该多接触英文,可,~~我不懂英文~~ 我更喜欢待在一个更熟悉的环境里啦。 ## ArkUI 你们的文档也是和 Apple 学的?ArkUI、SwiftUI、Jetpack Compose 以及基于 XML 视图的 Android 文档怎么都是一个样子? 这样才有教程书的生存空间是吧。 官方入门教程里的界面也太丑了吧,还是说 Harmony Design 就是这样的?实际上,我都不知道这算不算的上 Harmony Design,因为真的很丑。 我该怎么使用图标呢?我真的得将一堆 SVG 下载下来然后再作为资源文件使用吗?鸿蒙是有自己的图标库的,能否像 Flutter 或者 SwiftUI 那样更加和 ArkTS 结合起来呢? 我看到有 `Symbol{:ts}` 啦,但是一样,示例代码呢?后面是找到了示例代码,但现在要我再去找一次,那我真不知道在哪里翻出来的示例代码。 ```ts SymbolGlyph($r('sys.symbol.ohos_trash')) .fontWeight(FontWeight.Lighter) .fontSize(96); ``` ```ts Text() { SymbolSpan($r('sys.symbol.ohos_trash')) .fontWeight(FontWeight.Normal) .fontSize(96) } ``` 我去,我怎么没有 `SymbolGlyph{:ts}` 和 `SymbolSpan{:ts}`,有版本要求吗?下次记得标注。 一样没有组件 Gallery 展示 Harmony Design 的默认组件样式,别学 Apple 啊,你能做的更好的啊。 ## 总结 累人。
## Swift 语言 [Swift](https://developer.apple.com/swift) 是 [Apple ](https://www.apple.com) 开发的一门编程语言 —— 不像 [某为](https://www.huawei.com) 什么 [ArkTS 语言](https://developer.huawei.com/consumer/cn/arkts) 就是给 [TypeScript](https://www.typescriptlang.org) 套皮 —— 用的范围也很小,就它自家的产品开发用。 Swift 和 [Kotlin](https://kotlinlang.org) 非常相似,创新了一些比较奇妙的语法比如: ```dart // Dart callFunction(parma1, (value) { final value2 = value * 2; print(value2); }); ``` 这种最后一个参数是函数时,可以写作: ```swift // Swift callFunction(parma1) { value in let value2 = value * 2 print(value2) } ``` 你说代码好看了嘛是好看了,但代码格式化时不会自动格式化到这种好看的格式,要写这种格式代码补全又不给我补全成这样,到后面反而是浪费了时间。 我不是很喜欢 Swift,究其原因如下: 1. 必须使用 Xcode 才能使用 Swift 语言 2. Xcode 不自带代码格式化,需要自己找插件 3. 格式化风格不统一 4. 没有热更新(Dart 都可以不依赖 Flutter 进行热更新) 在寻找 Swift 相关项目时看到了能使 Swift 热更新的 [InjectIII](https://github.com/johnno1962/InjectionIII) 项目,为什么 Apple 不加? > 2024-07-05 12:50:35 > > 修正:Swift 可以在 macOS、Linux、Windows 上使用,详见 [官方文档](https://www.swift.org/getting-started) > > 这下更喜欢 Swift 了 🥰 ## Xcode 我真的很想吐槽:这是人用的 IDE? 真的很难想象 Xcode 没有 Internationalization,以及它的那些面板排布为什么这么反人类,文件管理视图为什么这么让人憋屈。 我知道 Xcode 和 Android Studio 一样都有个项目视图,但 Android Studio 还能让人切到文件视图,但 Xcode,我的选项呢? `Preview` 功能是需要表扬的,因为 SwiftUI 不支持热更新所以连 `Preview` 都没有的话就更写不下去了。 但它这 `Preview` 是会丢失状态的,所以还是有点不行。 ## SwiftUI 我要骂死你们的 Document 啊,你们是不舍得给例子吗?光有文字描述我怎么知道我怎么使用这个组件、函数、类啊? `List` 也是神鬼莫测,文档不说明它会自动给子组件加背景和分割线,我在思考。 有个 `LabeledContent` 这么好的组件你怎么忍心让它吃灰呢?我一开始一直都是用 `HStack { Label() Space() Text() }{:swift}` 这样实现类似 Flutter 里的 `ListTile{:dart}` 组件的。 它要是像 Flutter 那样有一个 [组件 Gallery](https://flutter.github.io/samples/web/material_3_demo) 给你展示出来多好啊,可就是没有。 要称赞的一点就是它的 `Text` 组件,能直接写 Markdown 转 URL 链接: ```swift Text("[byrdsaron@gmail.com](mailto:byrdsaron@gmail.com)") ``` ## 总结 资料好少,我好伤心。 自己在用 SwiftUI 写一个手写字体创建软件,我要了解 [Unicode](https://home.unicode.org)、字体、字形的相关知识,特别是怎么在 SwiftUI 里实现这件事,因为这需要涉及到一些比较低级的函数和接口。 但资料少的一批,官方文档简略的一批,鼠鼠我伤心的一批 😢。
自写日记开始,自己就越来越注重文字排版。 我是希望自己编写出来的东西是被精心设计过的,被别人看到时别人会感到舒适的,所以会去了解、学习一些相关知识。 故在此摘录并补充如下来源的一些规则: - [中文文案排版指北](https://github.com/sparanoid/chinese-copywriting-guidelines) - [Requirements for Chinese Text Layout - 中文排版需求](https://www.w3.org/International/clreq) - [ASCII and Unicode quotation marks](https://www.cl.cam.ac.uk/~mgk25/ucs/quotes.html) ## 使用居中的省略号 > 其呈现上占两个汉字空间、包含六个省略点且在水平和垂直方向均位于字面正中,通常使用两个连续的 `U+2026 HORIZONTAL ELLIPSIS […]` 来实现。 > > 在 Unicode 标准第 14 版的 6.2 章中,也推荐使用 `U+22EF MIDLINE HORIZONTAL ELLIPSIS [⋯]` 作为省略号。 > > 此符号配合适当的转向与取代机制,在显示上无论直横排,省略点皆居中,更符合排版需求。 但据 [此评论](https://github.com/sparanoid/chinese-copywriting-guidelines/issues/58#issuecomment-355893405) 指出,后者是隶属于数学符号的 —— 应该就是 LaTeX 里 `\cdots{:latex}` 对应的字符 —— 加之 [此评论](https://github.com/sparanoid/chinese-copywriting-guidelines/issues/58#issuecomment-356473325) 指出 <Kbd>^</Kbd> 默认映射为前者,我个人还是会使用前者的。 本网站为实现居中省略号,特地使用了字形为居中样式的字体。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>注意</AlertTitle> <AlertDescription>暂未实装</AlertDescription> </Alert> ## 使用标准的专有名词 例如 GitHub,官方使用该词时都是 **G**it**H**ub,从来不会使用什么 github、gitHub。 Xcode 也是,c 是小写的,而 VSCode,C 是大写的。 当然,编程里有 `camelCase` 这样的命名规范,那么这时 GitHub 对应什么?是 `github` 还是 `gitHub` 呢? 有兴趣的读者可参见 [camelCase 英文维基百科](https://en.m.wikipedia.org/wiki/Camel_case) 中的 Programming and coding 一节。 我是这样想的,人家既然这样设计了,必然保留人家的特征是最好的。 在此列表列出个人会最终采用的命名: | 类别 | 命名法 | 例 | | :----------: | :-----------: | :------------------------------------: | | 专有名词 | - | GitHub、SurviRed、API、JSON | | 变量、函数名 | camelCase | `gitHub`、`surviRed`、`api`、`json` | | 类名 | PascalCase | `GitHubAPI`、`SurviRedJSON`、`APIJSON` | | 常量名 | CONSTANT_CASE | `SURVIRED_API` | | 文件名、URL | kebab-case | `github-json` | ## 不再过分使用括号 括号一层一层嵌套会使得意思极其“扭曲”,理解起来需要绕弯子,同时存在一堆右括号连在一起的情况,这很不美观。特别是如果存在括号内多重括号完后接下句,其所指的前文是很难很快找到的。 例文: > 我是知道但没心思听(我一向屏蔽东西还算厉害(不过上次周测理综(语文(?))考试时外面在办丧事,丧乐把我人搞没了)的),旁边的同学倒是听得津津有味。 更好的做法当然是尽可能不使用括号,将想要表达的内容尽可能展开(flatten)来,出现跳跃性的句子可以使用破折号。 修改: > 我是知道但没心思听 —— 我一向屏蔽东西还算厉害的,不过上次周测理综(语文?)考试时外面在办丧事,丧乐把我人搞没了 —— 旁边的同学倒是听得津津有味。 ## 中英文混排时添加空格 在绝大多数情况下,在半角字符和全角字符直接加入空格就能给人一种文章没那么挤的感受。 比如接下来的这句话: ```plaintext 我喜欢吃apple,不喜欢吃peach和orange。 ``` 加入空格: ```plaintext 我喜欢吃 apple ,不喜欢吃 peach 和 orange 。 ``` 这里在每个单词左右两边都加了空格。 但这里实际上 apple 和 orange 后面接续的是一个全角的标点符号,且这个标点符号视觉上可以看作一个半角符号和一个空格,所以我们可以把后面的空格删去。 ```plaintext 我喜欢吃 apple,不喜欢吃 peach 和 orange。 ``` 但像“——”“……”这种会占满整个宽度的标点符号,现在看来它们确实有点挤,建议加上空格。 这也带来了一个好处,让我说明白一些: 我们在编辑一段文本的时候,经常使用 <Kbd>←</Kbd> 或 <Kbd>→</Kbd> 来跳转光标,但是这过于的不方便。 而我们可以使用 <KbdGroup><Kbd>Ctrl</Kbd><span>+</span><Kbd>←</Kbd></KbdGroup> 或 <KbdGroup><Kbd>Ctrl</Kbd><span>+</span><Kbd>→</Kbd></KbdGroup> 进行快速跳转,对于像 Microsoft Word 这样的编辑器,其会智能的将中文词汇分段,所以在跳转时会跳到词的开头或结尾,而不是整个句子的开头或结尾。 而对于未实现中文分词的编辑器,加上的空格就作为了一个“跳板”,更加方便跳转。 ### 计量单位 1 kg,1 m,1 s。在数字和单位之间需要空格 —— 这实际上就是英文排版要求 —— 而类似 100%,百(千)分号不需要。 类似 4G(第四代移动通信技术)这样的词,它本身是一个专业名词,所以之间不需要空格,但 4 G 确实可以表示类似“四倍重力”“四个金币”的意思,所以这就得看上下文了。 同时说说苹果在这方面的细节,他们会如上细微调整半角和全角字符之间的间隔(kerning),看上去和加了空格差不多,反而因为自己加了空格可能会显得间隔过大。 但考虑到不是所有的设备都有这样的特性,自己加上空格还是更普适的。 ### 斜杠 在英文排版中,表示“或”的斜杠两边不需要空格,相当于将其认为 26 个英文字母中的一个(大雾)。 但在代码中,斜杠一般表示除法,两边需要空格,以提供更好的可读性。 ## 引号 - [直角引号 「」『』 源自哪里?](https://www.zhihu.com/question/19867627) - [请正确使用直角引号与西文引号](https://zhuanlan.zhihu.com/p/20151625) - [ASCII and Unicode quotation marks](https://www.cl.cam.ac.uk/~mgk25/ucs/quotes.html) 大家好 ,我们是 `“` `”` `‘` `’` `"` `'` `「` `」` `『` `』`,今天来点大家想看的东西啊。 ## 「或」 「A 或 B」是二选一?还是二者其一即可? 如果在数学、程序或逻辑学,那么「或(OR)」默认是后者,严谨来说叫「逻辑或」,而要表示前者,则会使用「异或(XOR)」来表示。 自然语言里,更加倾向于异或,但是具体还是得看上下文,比如上文的「在数学、程序或逻辑学」这句话,就表达的是逻辑或。 那么 A/B 呢?这实际上不强调二选一还是二者其一即可,甚至可能表达两者都必须要出现,表达的是 A ∧ B,比如 I/O。 总之,使用 OR 和 XOR 就能避免这种问题。
使用报告系列开新坑了,今天要谈的是 [Next.js](https://nextjs.org/docs) 14。为什么是 14 呢,因为我从 14 学的,别叫。 先做个介绍吧,最新的 Next.js 官网上其称自己为“The React Framework for the Web”,记得之前有多加一个“专为生产环境”的头衔,总之,人家是框架,开发的方方面面都体贴的为你想到了。 对了,可能还要再介绍 [React](https://react.dev/learn),它自己介绍自己为“JavaScript library”,在我看来,它就是将原先命令式的 JavaScript 操作,改为了更加简约的声明式组件,提升了组件的复用性。 对,大学课程里教过我们使用 [jQuery](https://jquery.com) 来操作 HTML 元素,但这玩意怎么还没死啊?这不累死个人?这不老古董? 以及,React 操作的是 [DOM](https://developer.mozilla.org/zh-CN/docs/Web/API/Document_Object_Model/Introduction) 节点,通过 `<Link>{:tsx}` 组件,其能在“跳转页面”时不再真正跳转页面,而是根据新获取的信息更新当前页面,直观来说就是浏览器左上角不再出现转圈圈的刷新图标,使单页应用成为可能。 我是不是还要再解释一下什么是 [单页应用](https://developer.mozilla.org/zh-CN/docs/Glossary/SPA)(?)。 ## 非常好路由 Next.js 一大好处就是基于文件系统的路由,它抹去了原 React 提供的注册路由的方案,以及其提供的动态路由。 具体的不细讲,但我应该说明一点,就是即便 [React Native](https://reactnative.dev) 也有基于文件系统的动态路由,我也不会喜欢 React Native,因为移动端是移动端,网页是网页,如果真喜欢网页这一套,那还不如真就 WebView 跑网页完事。 ## 组件设计 Next.js 是 React 的框架,所有为 React 开发的 UI 库都能在 Next.js 里使用(不像某个 React Native(指指点点.jpg))。 之前和谢佬参赛时使用的是 [MUI](https://mui.com) 下的 [Joy UI](https://mui.com/joy-ui/getting-started),但 React 的生态太广阔了,不局限于 Joy UI,自己转用了 [NextUI](https://nextui.org/docs/components/avatar) 和 [Ant Design](https://ant.design/components/overview-cn),前者和开发 Next.js 的 Vercel 公司没有任何关系,但 UI 看起来很像,后者则是蚂蚁集团开发的。 使用别人的组件基本上就按它们的文档来就行,它们提供的属性一般就足够了。 但我们还是有自己写点样式的,这里就不得不提到 [Tailwind CSS](https://tailwindcss.com) 了。 ## 组件的修改 内联样式如果使用 `style{:tsx}` 属性来配置,会变得极为冗长,Tailwind CSS 能大大改善这点,并对响应式的支持更好 —— 比如对界面大小的响应、暗黑模式的响应、打印状态的响应。 更不用说我不喜欢的外置 CSS 文件了。 ## 服务器组件和客户端组件 这我看过教程,但教程里的方法是 Next.js 14 之前的,我理解还是不太清楚,经常到了报错说要用 `"use client"{:tsx}` 时才反应过来。 这个还得再了解了解。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2025-01-05 18:48:20 补充</AlertTitle> <AlertDescription> Minecraft 中也分为服务端 mod 和客户端 mod,服务端不能调用客户端才拥有的 API,类比之下,只要是依赖用户浏览器的内容,就应该使用 "use client" </AlertDescription> </Alert> ## 状态管理和 Hook React 本身有带 [状态管理](https://react.dev/learn/passing-data-deeply-with-context) 和一些简单的 [Hooks](https://react.dev/reference/react/hooks),因为我在学 Flutter 时对 Flutter 本身自带的、也是通过 `context` 向上查找根组件保存的状态的 [状态管理](https://api.flutter.dev/flutter/widgets/InheritedWidget-class.html),以及 [flutter_hooks](https://pub.dev/packages/flutter_hooks) 包里的 Hooks 有一些了解,或者说 Flutter 和 flutter_hooks 本身就从 React 学习了很多,我也就大致对 React 的状态管理和 Hooks 有了一些概念。 具体深造还是得靠写项目的,原理可以不清楚,但总不可以不会用吗 —— 虽然说面试可能也会问到就是了。 和 Flutter 有社区的状态管理方案一样,React 也有其它的状态管理方案 —— [Redux](https://redux.js.org)(实际上 Flutter 社区就有 [同名包](https://docs.flutter.dev/data-and-backend/state-mgmt/options#redux)),但我不会用。 而且据谢佬说这东西太复杂了,给我推荐了 [zustand](https://github.com/pmndrs/zustand),到时候都学学看就是了。 而 Hooks 方面,我不太理解 `useEffect{:tsx}` 是用来干什么的,感觉 `useState{:tsx}` 就足够了 —— 我看 `useEffect{:tsx}` 的一个应用的网络请求,但我明显找到了一个更牛逼的 Hooks —— [useSWR](https://swr.vercel.app/zh-CN/docs/getting-started),其也是由 Next.js 背后的同一团队创建的。 真的非常有用这玩意。 ## 总结 Next.js 和 React 的组合非常适合网页开发,可能之后学习 [Vue](https://vuejs.org) 的时候会再来一个它们间的对比,所以说本报告肯定会有第二期。
被恶心到了,我要狠狠的吐槽。 最近在恶补 React、Next.js、React Native,我先谈谈这个 React Native。 ## 语言不行? 几个月下来,对 [TypeScript](https://www.typescriptlang.org) 的了解更深了,能基本使用 TypeScript 了,像是它的解构,挺有趣的。自己也用 TypeScript 开发了一个 [VSCode 插件](https://github.com/Cierra-Runis/based_vscode_extension),可以说是这个项目后才对 TypeScript 有了好感。 有关它的类型,我还是不太能看懂,特别是我想要知道一个类型到底是怎样的时候,也就是翻源码的时候,要在很多联合类型直接跳转,这挺麻烦的。而之前也谈过,[Dart](https://dart.dev) 很直观,没有这么绕 —— 但我也确实想要 Dart 加入联合类型就是了。 对了,补充一点,之前说到 Java 没有空安全检查,这不太对,因为后面较新版本的 Java 有空安全,我也看到有的 Java 使用了 `@Nullable{:java}` 注释。 我不确定现在公司里都用的什么版本的 Java,不会还是 Java 8 吧?我是建议一直跟最新的,不管是语言还是框架,它们为什么要更新呢?因为它们加入了一些新东西,这些东西肯定是被好好讨论后才加入的,而被 deprecate 的那些东西,终将是会被删掉的,不升级还不行。新版本一般也会修复一些 bug、提升些性能,向后兼容的版本范围也可能变小,总之更新是好事。 但也要求这个过程是渐进的,不然出 bug 会很难受,比如说 Windows 升级,我甚至不想让它自动更新。 ## 框架不行? ### 组件设计 这个我还是要批评的,基础组件太少,布局写起来很麻烦。 这时候我就去找组件库,找到个 [React Native Paper](https://reactnativepaper.com) 库,用的是 [Material Design 3](https://m3.material.io) 的设计,但也没有像 Flutter 里 `Scaffold{:dart}` 的存在,凑合凑合还算过得去。 ### 组件修改 样式确实可以不放在另一个文件夹里,能写内联的,在 React Native 里经常使用 `style{:tsx}` 属性修改,在谈 Next.js 我还会再说个 Tailwind CSS。 Lint 提示确实还是不太好,有些属性名和原来的 CSS 属性名还有区别,我可不想被累死。 ### 组件在多平台下的表现 这个我就不多谈了,React Native 表现挺差的,但我现在只搞 Android 这边的,随他去吧。 ### Navigation 导航 我草死你的妈啊 😅,难用一匹 —— 我现在使用的是 [@react-navigation](https://reactnavigation.org/docs/getting-started) 这个包。 首先,我还是不喜欢命名路由,对 Flutter 来说一样。第一这意味着路由名称是硬编码的字符串,一旦重构会很麻烦;第二传参变得毫无类型可言,我该怎么判断它有没有我要的参数,我难道要每个需要传参的页面(路由、提示框)里都写 `as{:tsx}`?而且我如果修改了参数类型,在 `navigation.navigate{:tsx}` 这边是不会有任何提示的。 对了,这个 `navigate{:tsx}` 函数本身的类型好像有问题,不知道为什么它要求的是 `never{:tsx}`,而我需要传入字符串和给页面的传参,但是它也只是有个 lint 报错在那,用还是能用。 再就是这个在 Flutter 里称作 `AppBar{:dart}` 的东西 —— 谁要你自动给我每个路由里的界面都带上了?但这样我人又懵了,对哦,那我自己要写 `AppBar{:dart}` 对吧,嗯,React Native Paper 里有个叫 `Appbar{:tsx}` 的东西,挺好的 …… 等一下,返回按钮不是自动 implement 的,因为这两个包直接没有关系。也就是说我还要自己写一个 `AppBar{:tsx}` 组件,自己看看这个组件上级有没有路由,有就像 Flutter 那样自动 implement。 唯一一点好处就是,这个页面间跳转动画挺好看,因为跳转动画是 Android 自带的,因为跳转是使用了原生的。 ## Debug 工具不方便 对,今天开个第三节继续吐槽 React Native。 我是使用 VSCode 和 React Native Cli 进行开发的,还使用了 Microsoft 开发的一个插件。 首先恶心人的地方是启动,不能 <Kbd>F5</Kbd> 启动(或者说我不知道怎么配置),要 <KbdGroup><Kbd>Ctrl</Kbd><span>+</span><Kbd>Shift</Kbd><span>+</span><Kbd>P</Kbd></KbdGroup> 在面板里选择。这还行,但接下来我人晕了,VSCode 没有进入调试模式 —— 就是底下状态条没黄,这说明它没有 VSCode Debugger,这?(刚找到篇 [文章](https://blog.logrocket.com/debugging-react-native-vs-code) 说有插件能,等我用了之后再补充) 我出错了不知道具体错误在哪,鼠标不会自动跳到出问题的代码去, 而且我这玩意不能热重启,我只能重载 VSCode 再启动 —— 而热更新也是,很多时候我都不知道它有没有更新,特别是在出 bug 后,保持黑屏,还得自己重启。 ## 结尾 总之写起来很累,相比较 Flutter,无论是布局、导航、编程语言、调试工具,React Native 都没有很大的优势 —— 它最大的优势可能就是沾了 React 的光,“熟悉 Web 前端开发的技术人员只需很少的学习就可以进入移动应用开发领域”,但 React 嘛,还是让它好好搞网页开发吧,移动应用真不适合。 PS:本报告可能会有第三期。
## 怎么这么多东西  | 名称 | 介绍 | 名称 | 介绍 | | :-------------------------: | :----------------------------------: | :------------------: | :-------------------------: | | [GitLab] | 代码托管平台 | [JetBrains 全家桶] | 一堆 IDE | | [JetBairns AI] | AI 代码生成 | [Visual Studio Code] | 微软的轻量级代码编辑器 | | [Visual Studio] | 适用于大型项目的 IDE | [JetBrains Fleet] | AI 代码生成 | | [GitHub Copilot] | AI 代码生成 | [GitHub] | 全球最大代码托管平台 | | [Vue] | 网页开发框架 | [Vite] | 一款构建工具 | | [Android Studio] | 安卓开发 | [XCode] | Apple 生态下的 IDE | | [DevEco Studio] | HarmonyOS 应用 IDE | [Unity] | 游戏引擎 | | [团结引擎] | Unity 中国版 | [Qt] | C++ 跨平台开发框架 | | [Electron] | 基于网页的跨平台开发框架 | [Tauri] | 基于网页的跨平台开发框架 | | [React] | 网页开发 JavaScript 库 | [Cocos] | 国产游戏引擎 | | [Unreal Engine] | 游戏引擎 | [.NET] | .NET 跨平台开发框架 | | [七牛云] | 云储存、云计算服务 | [Codeberg] | 代码托管平台 | | [Stack Overflow] | 开发问答求助网站 | [Node.js] | JavaScript 后端技术 | | [Angular] | 与 React、Vue 并列的第三类方案 | [Bitbucket] | 代码托管平台 | | [微信小程序] | 微信小程序 | [Chromium] | 开源浏览器内核 | | [Firefox Developer Edition] | 火狐浏览器开发者版本 | [NervJS] | 京东的类 React 网页开发框架 | | [Taro] | 支持 React/Vue/Nerv 等用于小程序开发 | [Reqable] | 类 Postman API 调试应用 | | [Gitee] | 幽默国产类 GitHub 代码托管平台 | [Flutter] | Dart 跨平台应用开发框架 | | [npm] | Node 包管理器,处理依赖 | [Firebase] | 谷歌一站式后端服务 | | [Gradle] | 构建工具,用于 Java/Kotlin/Android | [CODEPEN] | 网页前端代码设计分享网站 | | [eclipse] | 一款已经不怎么好用的 IDE | | | [GitLab]: https://about.gitlab.com/ [JetBrains 全家桶]: https://www.jetbrains.com/ides/ [JetBairns AI]: https://www.jetbrains.com/ai/ [Visual Studio Code]: https://code.visualstudio.com/ [Visual Studio]: https://visualstudio.microsoft.com/ [JetBrains Fleet]: https://www.jetbrains.com/fleet/ [GitHub Copilot]: https://github.com/features/copilot/ [GitHub]: https://github.com/ [Vue]: https://vuejs.org/ [Vite]: https://vitejs.dev/ [Android Studio]: https://developer.android.com/studio [XCode]: https://developer.apple.com/xcode/ [DevEco Studio]: https://developer.huawei.com/consumer/cn/deveco-studio/ [Unity]: https://unity.com/ [团结引擎]: https://unity.cn/tuanjie/tuanjieyinqing [Qt]: https://www.qt.io/ [Electron]: https://www.electronjs.org/ [Tauri]: https://tauri.app/ [React]: https://react.dev/ [Cocos]: https://www.cocos.com/ [Unreal Engine]: https://www.unrealengine.com/ [.NET]: https://dotnet.microsoft.com/ [七牛云]: https://www.qiniu.com/ [Codeberg]: https://codeberg.org/ [Stack Overflow]: https://stackoverflow.com/ [Node.js]: https://nodejs.org/ [Angular]: https://angular.io/ [Bitbucket]: https://bitbucket.org/ [微信小程序]: https://developers.weixin.qq.com/miniprogram/dev/framework/ [Chromium]: https://www.chromium.org/ [Firefox Developer Edition]: https://www.mozilla.org/en-US/firefox/developer/ [NervJS]: https://github.com/NervJS [Taro]: https://taro-ui.jd.com/ [Reqable]: https://reqable.com/ [Gitee]: https://gitee.com/ [Flutter]: https://flutter.dev/ [npm]: https://www.npmjs.com/ [Firebase]: https://firebase.google.com/ [Gradle]: https://gradle.org/ [CODEPEN]: https://codepen.io/ [eclipse]: https://www.eclipse.org/
最近邀请我参加一个七牛云的校园编程竞赛,我觉得自己能学到些什么,所以就半同意下来了。 昨天晚上三个人简要谈了谈之后,说是要决定一下选什么框架好,目前就两个方向 —— [React Native](https://reactnative.dev) 和 [Flutter](https://flutter.dev),前者是我只听说过但没实际了解的东西,后者则是自去年 11 月份就在学的东西。 于是昨天配置好 React Native 的基础环境后,今天就看教程去了,但是嘛,越看就越觉得 React Native 不好用,我来具体分析一下。 ## 语言不行 首先,React Native 使用 JavaScript 或 TypeScript 语言来编写程序,而前者 JavaScript 是我认为最令人难受的语言 —— PHP 好像也挺垃圾的 —— 它的变量类型可以说是一塌糊涂,动态类型 Python 也有,但 Python 我就用来写点小东西,要我用它开发程序 …… 我也不是没写过,WordCloud 就是用 Python 写的,体验也是非常糟糕。除此之外我还非常讨厌它有 `=={:tsx}` 和 `==={:tsx}` 的区别,隐式转换是坏文明。 后者 TypeScript 我就直白的说,我看不懂! Python 里加入类型检查的方法是在变量后面冒号然后一个类型,而且重要的是,即便没给全部的变量都加上类型,程序仍然能跑起来,相当于只是给个 lint 提示一下,但 TypeScript 要写类型就得全部写完,类型还不直观,之前学 React 的时候想转 TypeScript 都转不了,后面对 React 就没多大兴趣了。 再来聊聊 Flutter 使用的语言 Dart,这是我用的最喜欢的一门语言。  首先,他非常像 Java,而我曾经写过一段时间的 Java 程序,所以很快就上手了。而且相比 Java,它有空安全检查,也就是一个变量只有在其类型后面接上个问号时才能赋值为 `null{:dart}`。 相比之下,Java 就没有这样的要求,就容易抛出空指针错误。它的语法比 Java 简约,`new{:dart}` 关键字不再是必要的。它还有动态类型,所以动态类型的好处 Dart 也有。 其次,我非常喜欢它的 `extension{:dart}` 方法,可以在已有的一个类,如 `DateTime{:dart}` 里,“注入”自己需要的一些便捷方法,这是非常好的,[pub.dev](https://pub.dev) 上还有一个包专门收录了许多的 `extension{:dart}`,极大方便了开发。 ## 框架不行 ### 包管理 React 和 React Native 都会搞出一个极大的 `node_modules` 文件夹,这是非常屎的一个设计,我就不多吐槽了,yarn、pnpm 都是为了解决这个烂玩意的,见 [此博客](https://gadzan.com/npm-yarn-pnpm)。 而 React Native 一个令我难受的点是,其 `core` 核心组件太少了,像是 Navigation 导航都要引入一个包,听说之前它是在 `core` 里的,之后被分离出去了 …… 嗯 …… 再来聊聊 Flutter 的包管理,它没有什么外置的包管理器,要么一句 `flutter pub add <包名>{:bash}` 解决,要么自己在 `pubspec.yaml` 文件里添加一行 `<包名>: <版本号>{:yaml}` 就行,甚至版本号都不填,留个冒号在那里,Flutter 自己会获取最新且兼容的包,一手包办的感觉太爽了。 那 Flutter 的包是放在哪的呢?如果使用 Windows,则在 `%LOCALAPPDATA%\Pub\Cache\hosted` 下,它按源的不同,分多个文件夹,一般来说是 `pub.dev` 文件夹和 `pub.flutter-io.cn` 文件夹,进 `pub.dev` 文件夹能看到很多包的不同版本的文件夹,就统计下来连 2 GB 都没有。 ```powershell PS > "{0} MB" -f [math]::round((Get-ChildItem -Path "$env:LOCALAPPDATA\Pub\" -Recurse | Measure-Object -Property Length -Sum).Sum / 1MB, 2) 1301.09 MB ``` 高下立判。 ### 组件设计 React 和 React Native 的类组件和 Flutter 的组件非常相似,但没有明显区分自己管理状态和无状态的组件,换言之,都是继承自 `Component{:tsx}`,都有一个 `state{:tsx}`,只是看你用不用就是了。 相似的点在于,前者的 `constructor{:tsx}` 相当于后者的 `initState{:dart}`,前者的 `render{:tsx}` 相当于后者的 `build{:dart}`,生命周期非常相似。 Flutter 是分了 `StatelessWidget{:dart}` 和 `StatefulWidget{:dart}` 的,前者只会要重写一个 `build{:tsx}` 方法,后者则是可重写整个生命周期。 ### 组件的修改 这是我很不喜欢的一点,所有的,对于一个组件的修改,都要在一个远离组件的一个键值对里配置,这非常割裂。 其实我在学 HTML 和 CSS 的时候就有这样的感觉,样式为什么要放到另一个文件里?紧靠着不是更方便吗?没办法,网页这样搞是历史原因,React 也是搞网页的所以能理解,但 React Native 的话 …… 当我知道它不是在各平台的 WebView 里跑 React 时我就不理解了。 而且写的配置,对 `key` 是没有 lint 提示的,我鼠标移到上面,它不会提示我这个组件有哪些可以修改的属性,加重了记忆负担,而 `value` 更是离谱,绝大多数都是字符串,都是同一个类型,要是打错了怎么办,要是没有代码补全怎么办? 相比之下,Flutter 的组件的配置要更加舒服,在其构造函数里填入配置的属性即可,而且 lint 会显示构造函数的参数和参数类型,还有 [Dart Doc](https://dart.dev/tools/dart-doc) 显示示例。除此之外,全局的主题配置也是可以的,像是 `MaterialApp{:dart}` 就有 `theme{:dart}` 属性,给其子组件树应用上。 ### 组件在多平台下的表现 React Native 说是一套代码跑多个平台,但我觉得它的表现不尽人意,多平台的表现差距太大。就拿圆形加载器组件举例,大小属性值怎么可以只在安卓有效? 这是受到原生组件的限制导致的,iOS 没有大小属性值 …… 而 Flutter,实际上也有多平台适配,部分已多平台适配的组件如 `AlertDialog{:dart}` 是有个 `adaptive{:dart}` 方法的,而且不会有“受原生组件限制”这一说法。 ### Navigation 导航 我人都麻了,不知道是不是我会错意了,所有进入路由的组件都要受改造,还要在 `Navigation{:tsx}` 根组件里登记命名路由? Flutter 哪来那么多事,在 `MaterialApp{:dart}` 的 `home{:dart}` 属性填初始路由 —— 也就是 `"/"{:dart}` 的命名路由 —— 再用 `Navigator.push{:dart}` 方法压入未命名的路由,或者和 React Native 类似地在 `MaterialApp{:dart}` 填命名路由,然后用 `Navigator.pushNamed{:dart}` 方法压入命名路由。 灵活性比 React Native 强太多了。 ## 我了解不够 这里是我自己的一些问题,以上都是刚接触一天所体验到的,可能了解上面的一些问题也早都有了解决方案。
## 介绍 [LaTeX](https://www.latex-project.org) 是一个文档准备系统(Document Preparing System),它非常适用于生成高印刷质量的科技类和数学类文档。它也能够生成所有其他种类的文档,小到简单的信件,大到完整的书籍。LaTeX 使用 [TeX](https://www.tug.org/svn/texlive) 作为它的排版引擎。 总之是以代码的形式生成很漂亮的 PDF 文档!相比 Microsoft Word 它虽然不够直观,但,漂亮决定一切((( ## 使用 你以为我会教你怎么安装吗?当然不会,可以去谷歌一下。 但你说我真的喜欢 LaTeX 吗?实际上 LaTeX 体积过于庞大,而且总给我一种这仍是上个世纪的产物(它确实是),生硬,但又忠实的反应了其结果。 相比 LaTeX,更常用的是 [Markdown](https://daringfireball.net/projects/markdown),Markdown 的语法简单,扩展性强,只是想要个数学公式功能的话 Markdown 也能很好的胜任。 但 Markdown 并没有一个统一的语法,就比如 `_斜体_{:markdown}` 和 `*斜体*{:markdown}` 其结果都是 _斜体_ 一样,这就导致了各种 Markdown 渲染器的渲染结果有所不同,更不用说一些平台的扩展语法了。 那 Markdown 的创始人在干什么? ## 一些不便 1. Emoji 插入不便 2. 自定义字体不便 3. 错误排查不便 ## 参考链接 [UTF-8 characters in math mode](https://tex.stackexchange.com/questions/270154/utf-8-characters-in-math-mode)
## 缘起 在使用 Python 写监听器的时候经常使用邮件提醒监听器变化,一开始就是简单一句话提醒就行,后面想着这玩意应该能和自己以前收到的邮件一样好看,所以开始试着发送 HTML 格式而不是纯文本的邮件,经过一番折腾,最后搞出来了个 Python 包 [listener_email](https://github.com/Cierra-Runis/listener_email)。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>注意</AlertTitle> <AlertDescription>现已删除</AlertDescription> </Alert> ## 问题 参考了苹果购物详情邮件: 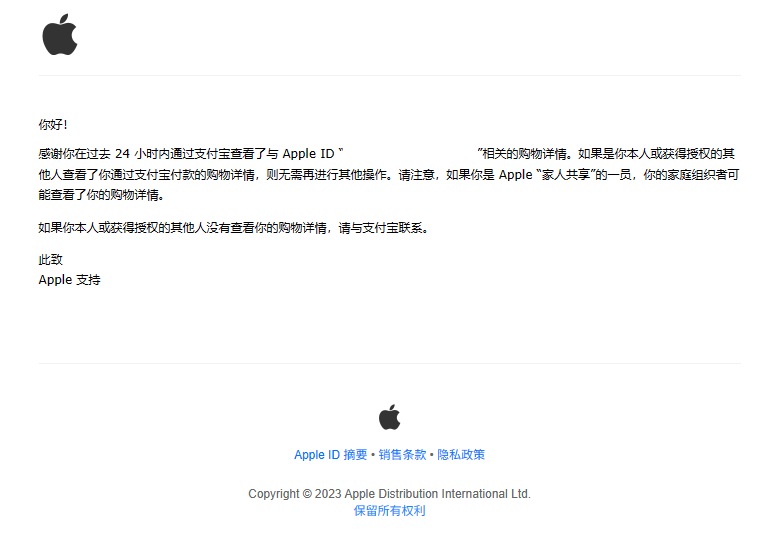 可是在修改过程中发现各个平台显示出的结果都不一样,其中: - QQ 邮箱网页版支持最好,能不使用 `<table>{:html}`、`<tbody>{:html}`、`<tr>{:html}`、`<td>{:html}` 等标签,而是普通的 `<div>{:html}` 和 CSS 里的 `display: flex{:css}` 属性进行布局,其他的邮箱都不可以;能使用 `github.com` 域名下的图片,而不是非要使用 `raw.githubusercontent.com` 域名下的图片,其他的邮箱都不可以;唯一的缺点是没有暗色模式 - iPad 版 Gmail 只能使用 `<table>{:html}`、`<tr>{:html}`、`<td>{:html}` 等标签进行布局,使用 `<tbody>{:html}` 标签 Gmail 会把里面的东西掏出来,从而破坏布局,且不支持自定义字体 - 网页版 Gmail 同上,但背景强制显示为白色,即便开启了暗色模式 - iPad 自带 `邮件` 同上,同时在 `系统设置 > 邮件 > 隐私保护` 里的 `保护“邮件”活动` 若未关闭,且下方 `阻止所有远程内容` 未关闭,则默认不能查看图片 - QQ 手机版 `QQ 邮箱提醒` 里的邮件不支持自定义字体,且若在 `QQ 侧拉栏设置 > 通用 > 模式选择` 里选择 `体验模式` ,则背景强制显示为白色,反之选择 `普通模式` 则背景在夜间模式下能显示为黑色 - 微信 手机版 `QQ 邮箱提醒` 里的邮件最差劲,不会自动识别邮箱为链接,不支持自定义字体,链接颜色会被一致改为蓝色,整个页面根本没做暗色模式,连上面 `发件人` 的样式都丑的一批,鉴定为“小而美” <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2025-01-05 21:44:39 补充</AlertTitle> <AlertDescription> 在最新的 iPadOS 18.2 中,只要在 `系统设置 > 邮件 > 载入远程图像` 启用即可 </AlertDescription> </Alert> 排查了好久才总结出以上信息,最后才写出来一个较为满意的 HTML ,想着这东西可以写成个包方便使用,也就开始了写包历程。 ## Python 包 答案是国内资源太少,姑且把包 [listener_email](https://github.com/Cierra-Runis/listener_email) 上传使用了。 但我想着一般包都是 `import listener_email{:python}` 然后 `listener_email.sent_email(){:python}` 来使用函数,而不是 `from listener_email import sent_email, ListenerEmail{:python}` 然后 `sent_email(){:python}` 来使用函数 …… 不懂,暂且懒了 ——
## 符号链接与云盘同步 在之前的 [云盘同步及 Obsidian 相关](/post/Cloud-Drive-Sync-And-Obsidian-Related) 文章里有提到: > 兜兜转转还得是微软的 OneDrive,在 cmd 使用: > > ```bash > mklink /d "D:\OneDrive\Songs" "D:\osu\Songs"` > ``` > > 创建链接使 `D:\OneDrive` 这个我个人设定的 OneDrive 文件夹(默认在哪来着不记得了)里出现一个 `Songs` 文件夹,进去一看好家伙是 `D:\osu\Songs` 里的东西,这样 Windows 方面成功。 其中使用的指令创建了一个符号链接,其中真正的文档处在后者 `D:\osu\Songs` 中,而前者 `D:\OneDrive\Songs` 是指向后者的一个符号链接,注意前者原先是不能存在 `Songs` 文件夹的,否则无法创建符号链接。 这种方案这会引发 OneDrive 无法正确显示是否已同步文件的问题,解决办法是先转移文件到别的地方,右键删除符号链接: > 在网上查询了许多方法都不管用,会出现删除后无法创建同名文件夹,文件夹会自动添加 `2` 后缀的 bug,感觉没死一样阴魂不散。 > > 解决办法是直接将符号链接改名为一串极度不会重复的名称(乱打即可)后右键删除,这样就能新建同名文件夹 并将文件转移至网盘,再使用 `mklink /d "D:\osu\Songs" "D:\OneDrive\Songs"{:bash}` 即可。 ## 符号链接与 VSCode 和 Git 根据以上步骤网盘存储真实数据,使用处使用符号链接将我项目里的 `_post` 文件夹改为指向 iCloud 里的 `帖子` 文件夹后,用 VSCode 打开项目文件夹会看到 `_post` 文件夹后提示这是一个符号链接,和平常一样没有任何问题。 但问题出现在 Git 同步上,`git push{:bash}` 后并不会将符号链接所指向的文件夹上传至 GitHub,而是符号链接本身。 对于我来说这并不影响,因为我使用 `.release_tool/main.py` 进行构建并发布至两个仓库 —— 一个是源文件仓库,一个是构建后的 GitHub Pages 仓库。
<Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2025-01-05 22:08:10 补充</AlertTitle> <AlertDescription>本文内容已不合时宜</AlertDescription> </Alert> ## 旧版的不适应之处 首先,原先的主题已经很久很久没有实质性更新了,而且自己在自定义方面处处碰壁,于是开始寻找其他博客主题。 ## 新版的好处 首先,好看多了,很多地方也能进行自定义。自己还花了一点小钱在 [阿里云](https://www.aliyun.com) 买了个域名,现在这个网站既可以通过 [https://cierra-runis.github.io/](https://cierra-runis.github.io) 访问,也可以通过 [https://note-of-me.top](https://note-of-me.top) 进行访问。 当然,经过配置之后,现在: - [https://cierra-runis.github.io](https://cierra-runis.github.io) - [https://www.note-of-me.top](https://www.note-of-me.top) 都是重定向到了 [https://note-of-me.top](https://note-of-me.top) 的,有时前面 `www` 没被隐去的情况也存在就是了 除此之外,还使用了 [去不图床](https://7bu.top) 作为网站图片的图床,价格也是特别的亲民,对于大陆用户的速度有一定提升。 ## 需要解决的问题 因为自己也有使用 Obsidian 进行博客编辑的习惯,那么在 iPad 上编辑时上传图片就略显复杂,试着寻找插件解决问题罢。
之前在某个直播间看到有人在用一个看起来又是很新的玩意写 Markdown 于是非常好奇的下载了 [Obsidian](https://obsidian.md),在看到官方的同步价格贵的一批之后在直播间里进行吐槽获得了能自搭同步的情报,于是进行一个 iCloud 的利用~ ## iCloud 与 Obsidian 具体来说,苹果官方在 Windows 端推出了个 [云盘同步工具](https://www.microsoft.com/store/productId/9PKTQ5699M62),安装登陆后就能在电脑上看到已和 iPad 文件管理器中同步了的 iCloud 云盘一项,在 iPad 端的 Obsidian 软件里选择在 iCloud 创建仓库后,便能在 iCloud 云盘里看到 Obsidian 文件夹,进行软件配置、文件创建、修改、删除都会很快同步,当然 iCloud 有时抽风给你在那把文件高高挂起也不是不可能 😡。 个人觉得每月给 iCloud 交的 6 块钱特别的值,便宜好用就是值 —— 于是这同步空间可不能浪费,把自己原先囤积在电脑上的图片、音乐、文件都传了上来,算是减轻了因装了很多开发工具而臃肿不堪的电脑的压力。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2025-01-05 21:51:25 补充</AlertTitle> <AlertDescription>已转向 Google Drive,并放弃使用 Obsidian</AlertDescription> </Alert> 哦,原先想着自己的一些“私密文件”也传上来方便些,但因为 **举头三尺有神明**,铁拳还是有可能砸到云上贵州的,所以转向了其他云盘。 ## Google Drive Google Drive 因为一些懂得都懂的原因,是不能直接访问的,那么这里就可以很好保存“私密文件”。毕竟自己鉴赏这些东西时,也会同时使用技术手段进行一个维基百科的查、用 iPad 里特别好的 GoodNotes 进行一个笔记的做,也就给 GoodNotes 的备份网盘设定成了 Google Drive ~ ## OneDrive 与 MaterialFiles 和 FolderSync 前面主要还是关注 iPad 和 Windows 之间的文件同步,但很明显 Android 阵营也有话说。 自己有在玩 [osu!](https://osu.ppy.sh),它有官方 [stable](https://osu.ppy.sh/home/download) 版、[lazer](https://osu.ppy.sh/wiki/zh/Help_centre/Upgrading_to_lazer) 版,[MATRIX-夜翎](https://space.bilibili.com/305637715) 从 lazer 版 fork 出来所维护的 [mfosu](https://github.com/MATRIX-feather/osu) 版,摆烂好久都不更新再这样下去什么时候我自己 fork 一个来更新的 [osu!droid](https://github.com/osudroid/osu-droid) 版,其中我玩的是 Windows 上的 stable 版和 Android 上的 osu!droid 版。它们很好的一点就是文件层次是互通的,简单同步俩者的 `Songs` 文件夹即可。 <Alert variant='destructive'> <AlertCircleIcon /> <AlertTitle>2024-06-10 20:45:00 补充</AlertTitle> <AlertDescription> 现 Windows 已转向 lazer 版,且 lazer 版的铺面文件系统已经不一样了,不能简单同步 </AlertDescription> </Alert> 可就是这么简单的方案实现起来也很累人。 首先需要选择同步云盘,因为 iCloud 没有支持安卓,且 Google Drive 需要那样的技术手段,便考虑别的方法。 在这里其实有另一套方案,这里我没有继续下去的原因就是有点晕人,再就是速度有点慢,但姑且也作一个记录。在 bilibili 里也能看见有介绍 [Syncthing](https://syncthing.net) 这款软件的视频,特点是 [P2P](https://en.wikipedia.org/wiki/Peer-to-peer) 安全迅速(存疑),设定双设备相互加对方好友并都设置目标文件夹后,只要连接成功就会开始同步,只可惜我这边连接不稳定 —— 仔细想想这也并不是很符合我的使用场景,这要求俩者都在线且成功连接,所以也就放弃了。 兜兜转转还得是微软的 OneDrive,在 cmd 使用: ```bash mklink /d "D:\OneDrive\Songs" "D:\osu\Songs"` ``` 创建链接使 `D:\OneDrive` 这个我个人设定的 OneDrive 文件夹(默认在哪来着不记得了)里出现一个 `Songs` 文件夹,进去一看好家伙是 `D:\osu\Songs` 里的东西,这样 Windows 方面成功。 问题出在 Android 方面,这边比 iCloud 不能自选任意文件夹同步更屑,连在文件管理器里都不显示 —— > 这里需点明的是不同安卓手机的文件管理器不一样,但自 Android 13 开始都是用底层的文件管理器才能打开 `data` 文件夹,在这个底层文件管理器里能看到 OneDrive 网盘,但也没什么用,没法管任意文件夹。 经过一系列的搜索,这里推荐 [MaterialFiles](https://github.com/zhanghai/MaterialFiles) 作文件管理器,[FolderSync](https://play.google.com/store/apps/details?id=dk.tacit.android.foldersync.lite) 作文件同步管理器。 前者是特别简洁的一款使用 [Material Design](https://m3.material.io) 风格的文件管理器,其几大特点分别是: - 能直接访问 `data` 文件夹 - 能使用 FTP 远程访问 - 安装包体积小至 8 MB,占用不超 20 MB 简而言之非常好用~ 后者则是能自选任意文件夹和超多同步云盘服务的文件同步管理器,具体的不介绍了,创建“文件夹对”进行文件同步即可 —— 虽然我文件快两万个同步起来确实有些吃力就是了。 ## 总结 苹果的东西在它自家用起来是很方便的,安卓的好处是自定义程度很高~什么 Windows?再好不过啦!
## Flutter 介绍 [Flutter](https://flutter.dev) 是 Google 推出并开源的移动应用开发框架,主打跨平台、高保真、高性能。开发者可以通过 Dart 语言开发 App,一套代码同时运行在 iOS 和 Android 平台。Flutter 提供了丰富的组件、接口,开发者可以很快地为 Flutter 添加 Native 扩展。 在此记录些常用资料: | 文档 | 文章 | | :--------------------------------------------: | :---------------------------------------------------------------------------------------------------: | | [官方网站](https://flutter.dev) | [Flutter 最佳实践和编码准则](https://ducafecat.com/blog/flutter-best-practices-and-coding-guidelines) | | [官方英文文档](https://docs.flutter.dev) | [iPad 大屏 & Flutter 多引擎适配之路](https://zhuanlan.zhihu.com/p/589939547) | | [官方中文文档](https://flutter.cn/docs) | [详解 android:elevation 的使用](https://www.python100.com/html/91048.html) | | [官方 Package 站](https://pub.dev) | [Flutter elevation 属性名称的含义](https://blog.csdn.net/gaoyp/article/details/123126394) | | [Flutter 实战](https://book.flutterchina.club) | [Android 中 elevation 的设置方法](https://www.jianshu.com/p/09959db18a4b) | | | [模式匹配](https://juejin.cn/post/7304930607133655059) | | 工具 | 包 | | :---------------------------------------: | :---------------------------------------------------------: | | [Json to Dart](https://jsond.bytex.space) | [图片缓存](https://pub.dev/packages/cached_network_image) | | | [BasedWidget](https://github.com/Cierra-Runis/based_widget) | | | [QWeatherIcons](https://pub.dev/packages/qweather_icons) | ## 使用 index.dart 文件简化导入 在 `lib/index.dart` 内 `export{:dart}` 所有子文件夹下的 `index.dart` 文件,其 `export{:dart}` 该文件夹下非自身的所有 `*.dart` 文件。 在所有 `*.dart` 文件,包括 `main.dart`,内尽绝大可能 `import 'package:<项目名>/index.dart';{:dart}` 即可简化导入。 同时当要引入外部包时,只要在 `lib/index.dart` 文件内导入即可,当然,有时会出现不同包之间的类名冲突,此时在需要使用到该包的地方单独 `import{:dart}` 即可,或者使用 `hide{:dart}` 或 `show{:dart}` 语法限制,具体例子如下: ```dart /// 各路由下的 index.dart export 'main.dart'; export 'pages/index.dart'; export 'widgets/index.dart'; /// flutter 相关 /// [RefreshCallback] 和 `export 'package:flutter/material.dart'` 冲突,两者近似 export 'package:flutter/cupertino.dart' hide RefreshCallback; export 'package:flutter/services.dart' show DeviceOrientation, SystemChrome; // 设备服务 /// [Badge] 和 `export 'package:badges/badges.dart'; // 小红点提示` 冲突,我想用外部包 export 'package:flutter/material.dart' hide Badge; export 'package:flutter/gestures.dart'; /// dart 相关 export 'dart:async' show Timer, StreamSubscription; export 'dart:convert'; export 'dart:io'; export 'dart:ui' show ImageFilter; /// 外部包相关 export 'package:badges/badges.dart'; // 小红点提示 /// [Interval] 和 `package:flutter/src/animation/curves.dart` 冲突,两者结构完全不同,但外部包里的这个用不到 export 'package:dart_date/dart_date.dart' hide Interval; // 日期工具 /// [Text] 和 `export 'package:flutter/material.dart` 冲突,两者结构完全不同,但外部包里的这个用不到 export 'package:flutter_quill/flutter_quill.dart' hide Text; // 富文本 ``` ## 版本号构建问题 Flutter 使用 `android/app/build.gradle` 来打包 APK, 且其引入了 `flutter.gradle` 并指向 `flutter.groovy`。 约在 `flutter.groovy` 的 `993` 行: ```groovy if (shouldSplitPerAbi()) { variant.outputs.each { output -> def abiVersionCode = ABI_VERSION.get(output.getFilter(OutputFile.ABI)) if (abiVersionCode != null) { output.versionCodeOverride = abiVersionCode * 1000 + variant.versionCode } } } ``` 我们知道 Flutter 将判断是否使用了 `'split-per-abi'{:bash}` 的 [Flag](https://oclif.io/blog/2019/02/20/cli-flags-explained), 是则在 `ABI_VERSION{:groovy}` 选择一个版本 `* 1000{:groovy}` 再加上构建号。官方解释见 [此链接](https://developer.android.com/studio/build/configure-apk-splits)。 我们只需修改 `ABI_VERSION map` 如下: ```groovy private static final Map ABI_VERSION = [ (ARCH_ARM32) : 0, (ARCH_ARM64) : 0, (ARCH_X86) : 0, (ARCH_X86_64) : 0, ] ``` **_注意若进行了 Flutter 版本更新,应重新修改该 `flutter.groovy` 文件_** ## Vivo 系手机无法调试 Flutter 程序 Vivo 系列手机升至 Origin3 后发现调试 Flutter 应用卡在启动页,并且没有任何报错,详见 [Github Issue](https://github.com/flutter/flutter/issues/117019),简化自 [此链接](https://blog.csdn.net/qq910689331/article/details/128790897)。 答案是 Vivo 发大病连日志都隐藏,我们需要提供 `IMEI 1` 码至 Vivo 官方进行授权 1. 拨号盘输入 `*#06#` 复制 `IMEI 1` 值 2. 添加企业 QQ 号 3002261823 或通过 [官方网站](https://dev.vivo.com.cn/connectus/customerService) 联系 3. 提交相关问题和信息,要求一键授权自己的手机 4. 等待授权成功后拨号盘输入 `*#*#112#*#*`,`右上角按钮 > 更多 > 一键授权` 即可 ## `AlertDialog` 的 `content` 传入 `ListView` 时在调试模式下报错 这是个怪问题,release 版本正常运行,解决方法如下: ```dart AlertDialog( title: (...), content: SizedBox( width: double.minPositive, // 可选 double.maxFinite 但建议为 double.minPositive, child: ListView( shrinkWrap: true, children: (...), ), ), contentPadding: (...), actions: (...), ); ``` ## Ard 语法 详见 [此页面](https://my.oschina.net/lemos/blog/5559979)。 ## 感想 - Flutter 的使用非常简单,上手也快,非常有意思。 - 自己用 Flutter 写了很多项目,这里来个 Mercurius 日记软件的 [仓库链接](https://github.com/Cierra-Runis/mercurius)。