June 30, 2024

高中数学

函数、导数、积分#

基本知识#

多阶导数的记法#

对 $f (x)$ ，记 $f^{'} (x)$ 为一阶导， $f^{''} (x)$ 为二阶导， $f^{'''} (x)$ 为三阶导，任意阶导都可为 $f^{(n)} (x)$

极值点判别法则#

对函数 $f (x)$ 在 $x = x_{0}$ 处若存在 $n \in N^{*}$ 使得

$f^{'} (x_{0}) = f^{''} (x_{0}) = \dots = f^{(n - 1)} (x_{0}) = 0$ ， $f^{(n)} (x_{0}) > 0$ ，则当 $n$ 为偶数时， $x_{0}$ 为极小值点

$f^{'} (x_{0}) = f^{''} (x_{0}) = \dots = f^{(n - 1)} (x_{0}) = 0$ ， $f^{(n)} (x_{0}) < 0$ ，则当 $n$ 为偶数时， $x_{0}$ 为极大值点

当 $n$ 为奇数时 $x_{0}$ 既不是极大值点，也不是极小值点

一般取 $n = 2$ ，即一般来说

$f^{'} (x_{0}) = 0$ ， $f^{''} (x_{0}) > 0$ 即有 $x_{0}$ 为极小值点

$f^{'} (x_{0}) = 0$ ， $f^{''} (x_{0}) < 0$ 即有 $x_{0}$ 为极大值点

注意 18 年全国三卷导数题（2）问

琴生不等式#

$\forall x \in D ， f^{''} (x) \geq 0 \Leftrightarrow \forall x_{1}, x_{2} \in D ， \frac{f ( x _{1} ) + f ( x _{2} )}{2} \geq f (\frac{x _{1} + x _{2}}{2})$

$\forall x \in D ， f^{''} (x) \leq 0 \Leftrightarrow \forall x_{1}, x_{2} \in D ， \frac{f ( x _{1} ) + f ( x _{2} )}{2} \leq f (\frac{x _{1} + x _{2}}{2})$

这在图像上显然成立，证明略

ALG 不等式#

$\forall x_{1}, x_{2} \in R^{*} \Rightarrow \frac{x _{1} + x _{2}}{2} > \frac{x _{1} - x _{2}}{ln x _{1} - ln x _{2}} > x_{1} x_{2}$

一个不等式#

(1) 若 $f^{'''} (x) > 0$ 且 $f (x)$ 有两零点 $x_{1}, x_{2}$ ，则 $f^{'} (\frac{x _{1} + x _{2}}{2}) < 0$

(2) 若 $f^{'''} (x) < 0$ 且 $f (x)$ 有两零点 $x_{1}, x_{2}$ ，则 $f^{'} (\frac{x _{1} + x _{2}}{2}) > 0$

现使用虚设函数法证明式 (1)

记 $g (x) = f (x) - f (a - x)$ ，其中 $a = x_{1} + x_{2}$ ，且令 $x_{1} < \frac{a}{2} < x_{2}$

则 $g^{'} (x) = f^{'} (x) + f^{'} (a - x)$

$g^{''} (x) = f^{''} (x) - f^{''} (a - x)$

$g^{'''} (x) = f^{'''} (x) + f^{'''} (a - x) > 0$

由 $g^{''} (\frac{a}{2}) = 0$ 得 $g^{'} (x) \geq g^{'} (\frac{a}{2}) = 2 f^{'} (\frac{a}{2})$

假设 $f^{'} (\frac{a}{2}) \geq 0$ ，则 $g^{'} (x) \geq 0$ ， $g (x)$ 单调递增

但 $g (\frac{a}{2}) = 0 \Rightarrow f (x_{1}) < f (x_{2})$ 与 $f (x_{1}) = f (x_{2}) = 0$ 的题设相悖

故 $f^{'} (\frac{a}{2}) < 0$ ，即 $f^{'} (\frac{x _{1} + x _{2}}{2}) < 0$

利用隐函数求导求曲线上一点切线斜率#

有 $F (x, y) = x^{2} + 2 x + y^{2} = 0$

则上一点 $(x, y)$ 切线斜率

$k = \frac{d y}{d x} = - \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} = - \frac{2 x + 2}{2 y} = - \frac{x + 1}{y}$

其中 $\frac{\partial F}{\partial x}$ 表示对 $F$ 求 $x$ 的偏导，即将除了 $x$ 的其他变量视为未知常数进行求导

同理 $\frac{\partial F}{\partial y}$ 表示对 $F$ 求 $y$ 的偏导

利用隐函数求导求约束条件下的函数最值#

已知约束条件 $F (x, y) = 0$ ，求 $G (x, y)$ 最值

例： $F (x, y) = x^{2} + y^{2} + x y - 4 = 0$ ，求 $G (x, y) = x^{2} + y^{2}$ 最值

解：令 $- \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} = - \frac{\frac{\partial G}{\partial x}}{\frac{\partial G}{\partial y}}$

化简得 $y = \pm x$

与 $F (x, y) = 0$ 联立解得 $(\pm \frac{2}{3}, \pm \frac{2}{3}), (\pm 2, \mp 2)$

可得代入得 $G (x, y)$ 最大值为 $8$ ，最小值为 $\frac{8}{3}$

不完全严谨，但确实很多时候有用。

圆锥曲线上一点切线方程#

方程	过 $P (x_{0}, y_{0})$ 的切线方程
$(x - a)^{2} + (y - b)^{2} = R^{2}$	$(x - a) (x_{0} - a) + (y - b) (y_{0} - b) = R^{2}$
$\frac{x ^{2}}{a ^{2}} + \frac{y ^{2}}{b ^{2}} = 1$	$\frac{x x _{0}}{a ^{2}} + \frac{y y _{0}}{b ^{2}} = 1$
$\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1$	$\frac{x x _{0}}{a ^{2}} - \frac{y y _{0}}{b ^{2}} = 1$
$\frac{y ^{2}}{b ^{2}} - \frac{x ^{2}}{a ^{2}} = 1$	$\frac{y y _{0}}{b ^{2}} - \frac{x x _{0}}{a ^{2}} = 1$
$y^{2} = 2 p x$	$y y_{0} = p (x + x_{0})$
$x^{2} = 2 p y$	$x x_{0} = p (y + y_{0})$

极值点偏移#

例： $f (x) = x (ln x - \frac{x}{2} + a - 1)$ 有两极值点 $x_{1}, x_{2}, x_{1} < x_{2}$

求 $a$ 范围
证明 $2 ln x_{1} + ln x_{2} < 0$

(1) 解：由 $f^{'} (x) = ln x - x + a$ ， $f^{''} (x) = \frac{1}{x} - 1$ 得

$f^{'} (x)_{ma x} = f^{'} (1) = a - 1$

由题 $f^{'} (x)_{ma x} > 0$ ，故 $a \in (1, + \infty)$

(2) 证：由 (1) 可得 $0 < x_{1} < 1 < x_{2}$ ，所证原式即 $x_{2} < \frac{1}{x _{1}^{2}}$

由 $0 < x_{1} < 1$ 得 $\frac{1}{x _{1}^{2}} > 1$

因为 $\frac{1}{x _{1}^{2}}$ 和 $x_{2}$ 都在 $(1, + \infty)$ 范围内

且 (1) 有 $f^{'} (x)$ 在 $(1, + \infty)$ 上单调递减

则所证 $x_{2} < \frac{1}{x _{1}^{2}}$ 即 $f^{'} (\frac{1}{x _{1}^{2}}) < f^{'} (x_{2}) = 0$

而 $f^{'} (\frac{1}{x _{1}^{2}}) = ln \frac{1}{x _{1}^{2}} - \frac{1}{x _{1}^{2}} + a$

其中的 $a$ 又可由 $f^{'} (x_{1}) = ln x_{1} - x_{1} + a = 0$ 得到

则代入得 $f^{'} (\frac{1}{x _{1}^{2}}) = ln \frac{1}{x _{1}^{2}} - \frac{1}{x _{1}^{2}} + x_{1} - ln x_{1}$

记 $g (x) = ln \frac{1}{x ^{2}} - \frac{1}{x ^{2}} + x - ln x = - 3 ln x + x - \frac{1}{x ^{2}}, x \in (0, 1)$

则证明 $g (x) < 0$ 即可

因为 $g^{'} (x) = \frac{( x - 1 ) ( x ^{2} - 2 x - 2 )}{x ^{3}} > 0$ 在 $(0, 1)$ 上成立

则 $g (x) < g (1) = 0$ ，故题得证

数列#

不动点的概念与性质#

一般对函数 $f (x)$ ，若 $\exists x_{0} \in R$ 使 $f (x_{0}) = x_{0}$ ，则称 $x = x_{0}$ 为 $f (x)$ 的一阶不动点

同时有 $f (f (x_{0})) = x_{0}$ ，易得一阶不动点也是二阶不动点

一般对数列 ${x_{n}}$ 有递推式 $x_{n + 1} = f (x_{n})$ ，若 $\exists x_{0} \in R$ 使 $f (x_{0}) = x_{0}$ ，则称 $x = x_{0}$ 为 ${x_{n}}$ 的不动点

易得若从某项 $x_{k}$ 为不动点则后数列恒定不变

要是数列 ${x_{n}}$ 中的项取不到不动点 $x_{0}$ ，但足够接近，且后来的项越来越接近 $x_{0}$ ，即收敛为 $x_{0}$

值得注意的是不动点可能为复数，也可能不存在

不动点的稳定性#

一阶线性递推数列#

即 ${x_{n}}$ 有 $x_{n + 1} = f (x_{n}) = p x_{n} + q$ ，求 ${x_{n}}$ 通项公式

$p = 1$ 时为等差数列
$p \neq = 1$ 时解方程 $x_{0} = f (x_{0})$ 得不动点 $x_{0} = \frac{q}{1 - p}$ 后，则 ${x_{n} - x_{0}}$ 为等比数列

分式递推数列#

即 $x_{n}$ 有 $x_{n + 1} = f (x_{n}) = \frac{a x _{n} + b}{c x _{n} + d}$ ，求 ${x_{n}}$ 通项公式

这里先解方程 $x_{0} = f (x_{0})$ 得 $c x_{0}^{2} + (d - a) x_{0} - b = 0$

当只有一解 $x_{0}$ 时， ${\frac{1}{x _{n} - x _{0}}}$ 为等差数列
当有俩解 $α, β$ 时（注意复数解也是两个）， ${\frac{x _{n} - α}{x _{n} - β}}$ 为等比数列

一般情形#

一般情形下先考虑解方程 $x_{0} = f (x_{0})$ 得到不动点 $x_{0}$

再在 $x_{n + 1} = f (x_{n})$ 两边同时减去 $x_{0}$

即 $x_{n + 1} - x_{0} = f (x_{n}) - x_{0}$

进行代数变形后一般能得到等差数列或等比数列形式

不动点为零、复数或不存在时#

为零时应当考虑倒数或增项后进行因式分解

为复数时数列必是周期数列

不存在时考虑其他方法

二阶线性递推数列#

即 ${x_{n}}$ 有 $x_{n + 1} = F (x_{n}, x_{n - 1}) = p x_{n} + q x_{n - 1}$ ，求 ${x_{n}}$ 通项公式，已知 $x_{1}, x_{2}$

设 $\exists a, b$ 使 $x_{n + 1} - a x_{n} = b (x_{n} - a x_{n - 1})$

有 $a + b = p, ab = - q$ ，即 $a, b$ 为 $x^{2} - p x - q = 0$ 的解

解得 $a, b$ 后，代入原先的等比数列，解得

$x_{n} = \frac{x _{2} - b x _{1}}{a - b} a^{n - 1} + \frac{x _{2} - a x _{1}}{b - a} b^{n - 1}$

一个求和式#

求 $i = 1 \sum n i \cdot i!$

注意到 $(n + 1)! = (n + 1) \cdot n! = n \cdot n! + n!$

故 $i = 1 \sum n i \cdot i! = i = 1 \sum n [(i + 1)! - i!] = (n + 1)! - 1$

构造函数证明数列不等式#

累加例#

求证 $i = 1 \sum n \frac{1}{i + 1} < ln (1 + n)$

解：利用 $a_{n + 1} = S_{n + 1} - S_{n}$ 试将 $ln (1 + n)$ 写成累加形式为 $i = 1 \sum n ln \frac{i + 1}{i}$

则试证 $\frac{1}{x + 1} < ln \frac{x + 1}{x}$ 对 $\forall x \geq 1$ 成立

记 $f (x) = ln \frac{x + 1}{x} - \frac{1}{x + 1}, (x \geq 1)$

$f^{'} (x) = - \frac{1}{x ( x + 1 ) ^{2}} < 0$

故 $f (x) > x \to + \infty lim f (x) = 0$

即 $\frac{1}{x + 1} < ln \frac{x + 1}{x}$ 对 $\forall x \geq 1$ 得证

故题得证

累乘例#

求证 $\frac{2}{n ( n + 2 )} < i = 2 \prod n ln i$

解：利用 $a_{n + 1} = \frac{T _{n + 1}}{T _{n}}$ 试将 $\frac{2}{n ( n + 2 )}$ 写成累乘形式为 $i = 2 \prod n \frac{i - 1}{i + 1}$

则试证 $\frac{x - 1}{x + 1} < ln x$ 对 $\forall x \geq 2$ 成立

下略，得题得证

由例可得我们可以通过寻找累加（乘）式以试证累加（乘）对应各项的大小，通过取值并求导得证后回推即题得证，避免了对构造函数不知所措。

向量#

基本知识#

向量点乘 $a \cdot b = ∣ a ∣∣ b ∣ cos θ$ ，其中 $θ$ 为向量 $a, b$ 所夹角的大小，几何意义略

二维向量伪叉乘 $∣ a \times b ∣ = ∣ a ∣∣ b ∣ sin θ$ ，其中 $θ$ 为向量 $a, b$ 所夹角的大小，几何意义为向量 $a, b$ 所夹平行四边形面积

两向量 $a, b$ 夹角为锐角的充要条件为 $a \cdot b > 0, ∣ a \times b ∣ \neq = 0$

两向量 $a, b$ 夹角为钝角的充要条件为 $a \cdot b < 0, ∣ a \times b ∣ \neq = 0$

叉乘#

二维#

叉乘应该主要是三维向量间的计算，我们先谈论其在二维中的应用

二维向量伪叉乘 $∣ a \times b ∣ = ∣ a ∣∣ b ∣ sin θ$

若 $a = [m n] = (m, n), b = [r s] = (r, s)$

则 $∣ a \times b ∣ = ∣ det ([m n r s]) ∣ = ∣ m n r s ∣ = ∣ m s - n r ∣$

其中 $det ()$ 用来求矩阵行列式，具体可看线性代数相关知识

通过上述介绍，我们可以很快求出两向量所夹平行四边形的面积

三维#

三维向量叉乘 $a \times b$ 所输出的是一个新的向量 $n$

其中 $∣ n ∣$ 等于向量 $a, b$ 所夹平行四边形面积， $n$ 为该平行四边形的法向量

且方向可右手掌心朝面，收起无名指和小指，中指指向自己，此时 $a$ 为食指， $b$ 为中指， $n$ 为大拇指

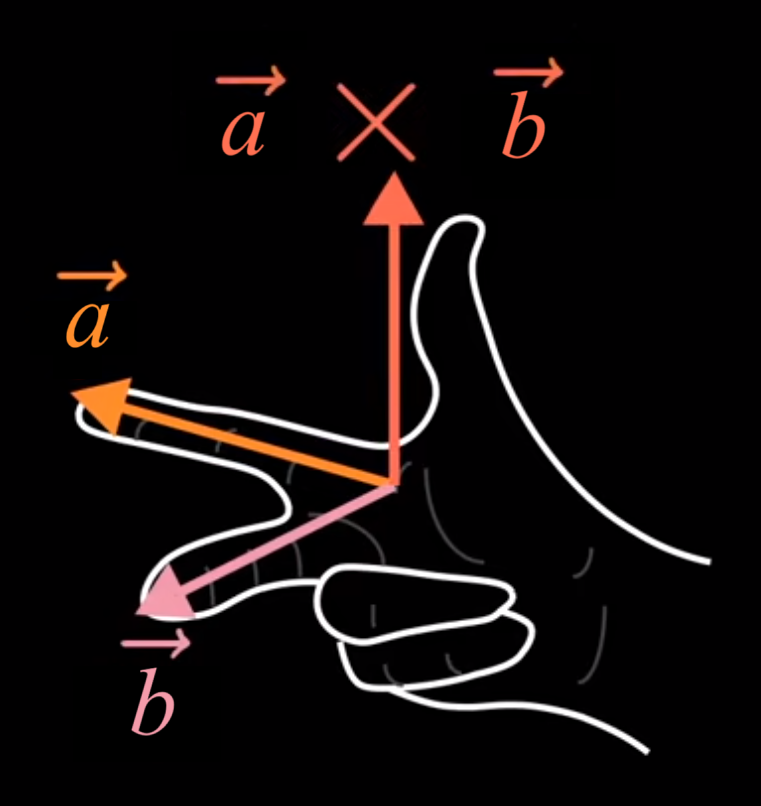
right hand

此处可注意到 $a \times b = - b \times a$

若 $a = a_{1} a_{2} a_{3} = (a_{1}, a_{2}, a_{3}), b = b_{1} b_{2} b_{3} = (b_{1}, b_{2}, b_{3})$

则我们列表 $a_{1} b_{1} a_{2} b_{2} a_{3} b_{3}$

则 $a \times b = (n_{1}, n_{2}, n_{3})$ 中

$n_{1}$ 为挡住所列表第一列后的行列式 $a_{2} b_{2} a_{3} b_{3}$

$n_{2}$ 为挡住所列表第二列后的行列式 $- a_{1} b_{1} a_{3} b_{3}$

$n_{3}$ 为挡住所列表第三列后的行列式 $a_{1} b_{1} a_{2} b_{2}$

通过上述介绍，我们可以很快求出法向量

立体几何中的应用#

求体积#

对于共起点的三维向量 $a, b, c$ 有以该向量所围成的平行六面体的体积 $V_{1} = ∣ (a \times b) \cdot c ∣$

所围成的三棱锥的体积 $V_{2} = \frac{V _{1}}{6}$

求二面角#

在求如 $E - A B - F$ 的二面角余弦值时，由于法向量求法不同而导致法向量夹角非二面角，要自主判断其正负，容易引发错误，现介绍一种方法避免错误：

求 $E - A B - F$ 二面角余弦

则平面 $A BE$ 一个法向量 $n_{1} = A B \times A E$

平面 $A BF$ 一个法向量 $n_{2} = A B \times A F$

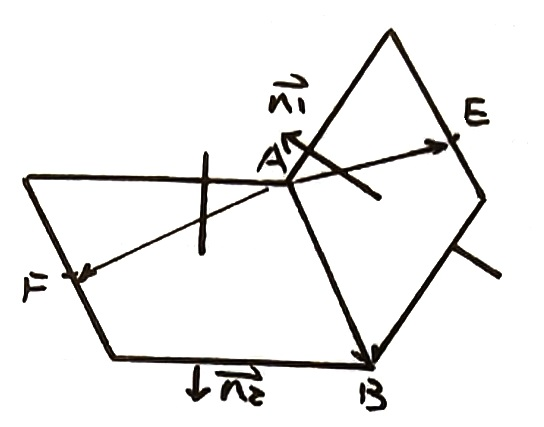
dihedral angle

则由图易得 $E - A B - F$ 即 $n_{1}, n_{2}$ 的夹角

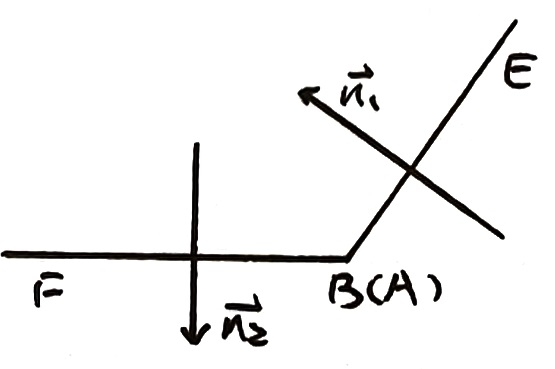
dihedral angle side

故可求得二面角余弦值

等和线、等差线、等积线、等商线、等平方和线#

等和线#

等差线#

复数#

复数四则运算的几何意义#

加法和减法略，我们着重介绍乘法

例： $(2 + i) \cdot i = - 1 + 2 i$

从复平面上看， $2 + i$ 逆时针旋转了 $\frac{π}{2}$

再例： $(3 + i) (1 + 3 i) = 4 i$

从复平面上看，两者辐角相加，模长相乘

证明：对复平面上一复数 $z$ 记模长为 $l$ ，辐角为 $θ$

则 $z = l cos θ + i \cdot l sin θ = l (cos θ + i sin θ)$

设 $z_{1}$ 对应 $l_{1}, θ_{1}$ ， $z_{2}$ 对应 $l_{2}, θ_{2}$

则 $z_{1} z_{2} = l_{1} (cos θ_{1} + i sin θ_{1}) \cdot l_{2} (cos θ_{2} + i sin θ_{2}) = l_{1} l_{2} [cos (θ_{1} + θ_{2}) + i sin (θ_{1} + θ_{2})]$

故得证

由上有复数相乘，模长相乘，辐角相加

同理有复数相除，模长相除，辐角相减

对于某些运算能缩短用时

复数的指数运算#

推广 $n$ 个复数相乘，有下式成立

k = 1 \prod n a_{k} + b_{k} i = k = 1 \prod n a_{k}^{2} + b_{k}^{2} \cdot [cos (k = 1 \sum n arctan \frac{b _{k}}{a _{k}}) + i sin (k = 1 \sum n arctan \frac{b _{k}}{a _{k}})]

其中 $a_{k}, b_{k} \in R, n \in N^{*}$

特殊的 $a_{k} = a, b_{k} = b$ 时

(a + b i)^{n} = (a^{2} + b^{2})^{n} \cdot [cos (n arctan \frac{b}{a}) + i sin (n arctan \frac{b}{a})]

更特殊的， $a = cos θ, b = sin θ$ 时

(cos θ + i sin θ)^{n} = cos n θ + i sin n θ

由二项式定理有

(cos θ + i sin θ)^{n} = k = 0 \sum n C_{n}^{k} cos^{n - k} θ (i sin θ)^{k}

拆项对应实部虚部得 $n$ 倍角公式

cos n θ = k = 0 \sum ⌊ n /2 ⌋ C_{n}^{2 k} (- 1)^{k} cos^{n - 2 k} θ sin^{2 k} θ

sin n θ = k = 0 \sum ⌊ n /2 ⌋ C_{n}^{2 k + 1} (- 1)^{k} cos^{n - 2 k - 1} θ sin^{2 k + 1} θ

其中 $⌊ n /2 ⌋$ 表示向下取整

圆锥曲线#

圆锥曲线与隐函数求导#

圆锥曲线上一点切线方程 —— 见利用隐函数求导求曲线上一点切线斜率

圆锥曲线外一点两切线切点连线（又称切点弦）形式同上

蒙日圆#

椭圆两垂直切线交点轨迹为定圆 $x^{2} + y^{2} = a^{2} + b^{2}$

焦点三角形面积#

对 $\frac{x ^{2}}{a ^{2}} + \frac{y ^{2}}{b ^{2}} = 1 (a > b > 0)$ 有 $S_{△ P F_{1} F_{2}} = b^{2} \cdot tan \frac{P}{2}$

对 $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1 (a > b > 0)$ 有 $S_{△ P F_{1} F_{2}} = b^{2} \cdot cot \frac{P}{2}$

抛物线无两焦点，无焦点三角形

通径#

对 $\frac{x ^{2}}{a ^{2}} + \frac{y ^{2}}{b ^{2}} = 1, (a > b > 0)$ 有通径长 $\frac{2 b ^{2}}{a}$

对 $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1, (a > b > 0)$ 有通径长 $\frac{2 b ^{2}}{a}$

对 $y^{2} = 2 p x, (p \neq = 0)$ 有通径长 $∣2 p ∣$

焦点弦#

对离心率为 $e$ 的圆锥曲线，过焦点的弦 $A B$ 与焦点所在轴交角若为 $θ$ ， $∣ A F ∣ = λ ∣ FB ∣$

则 $∣ e \cdot cos θ ∣ = ∣ \frac{λ - 1}{λ + 1} ∣$

结合三角函数和斜率 $k$ 可变形为其他形式

判别式#

对 $\frac{x ^{2}}{a ^{2}} + \frac{y ^{2}}{b ^{2}} = 1$ 与 $A x + B y + C = 0, (A \cdot B \neq = 0)$

相切 $\Leftrightarrow A^{2} a^{2} + B^{2} b^{2} = C^{2}$
相交 $\Leftrightarrow A^{2} a^{2} + B^{2} b^{2} > C^{2}$
相离 $\Leftrightarrow A^{2} a^{2} + B^{2} b^{2} < C^{2}$

对 $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1$ 与 $A x + B y + C = 0, (A \cdot B \neq = 0)$

相切 $\Leftrightarrow A^{2} a^{2} - B^{2} b^{2} = C^{2}$
相交 $\Leftrightarrow A^{2} a^{2} - B^{2} b^{2} < C^{2}$
相离 $\Leftrightarrow A^{2} a^{2} - B^{2} b^{2} > C^{2}$

费马定理与圆锥曲线的光学性质#

费马定理：光从一点传至另一点的用时总是最短（均匀介质中表现为路程最短）

假定圆锥曲线都为镜面，则

从圆心发出的光反射后总回到圆心
从椭圆一焦点发出的光反射后到另一焦点
从抛物线焦点发出的光反射后总是垂直于其准线
从双曲线焦点发出的光反射后所在直线过另一焦点

可以利用以上性质求某些距离和（差）的最值

且利用初中知识作切线和法线有反射角等于入射角

一个性质#

一动直线恒过圆锥曲线内一定点且交其于两点，则这两点切线交点在其外的某定直线上，反之也成立（与切点弦有相似之处）

对 $\frac{x ^{2}}{a ^{2}} + \frac{y ^{2}}{b ^{2}} = 1$ ，若定点为 $(x_{0}, y_{0})$ ，则定直线为 $\frac{x x _{0}}{a ^{2}} + \frac{y y _{0}}{b ^{2}} = 1$

对 $\frac{x ^{2}}{a ^{2}} + \frac{y ^{2}}{b ^{2}} = 1$ ，若定直线为 $A x + B y + C = 0$ ，则定点为 $(- \frac{A a ^{2}}{C}, - \frac{B b ^{2}}{C})$

对 $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1$ ，若定点为 $(x_{0}, y_{0})$ ，则定直线为 $\frac{x x _{0}}{a ^{2}} - \frac{y y _{0}}{b ^{2}} = 1$

对 $\frac{x ^{2}}{a ^{2}} - \frac{y ^{2}}{b ^{2}} = 1$ ，若定直线为 $A x + B y + C = 0$ ，则定点为 $(- \frac{A a ^{2}}{C}, \frac{B b ^{2}}{C})$

对 $y^{2} = 2 p x$ ，若定点为 $(x_{0}, y_{0})$ ，则定直线为 $y y_{0} = p (x + x_{0})$

对 $y^{2} = 2 p x$ ，若定直线为 $A x + B y + C = 0$ ，则定点为 $(\frac{C}{A}, - \frac{pB}{A})$